Note: This problem has almost the same setting as Problem B. Only the parts in bold in the main text and constraints differ.

You are holding a ring with both hands. This ring consists of $N\ (N \geq 3)$ parts numbered $1,2,\dots,N$, where parts $i$ and $i+1$ ($1 \leq i \leq N-1$) are adjacent, and parts $1$ and $N$ are also adjacent.

Initially, your left hand is holding part $1$, and your right hand is holding part $2$. In one operation, you can do the following:

• Move one of your hands to an adjacent part of the part it is currently holding. However, you can do this only if the other hand is not on the destination part.

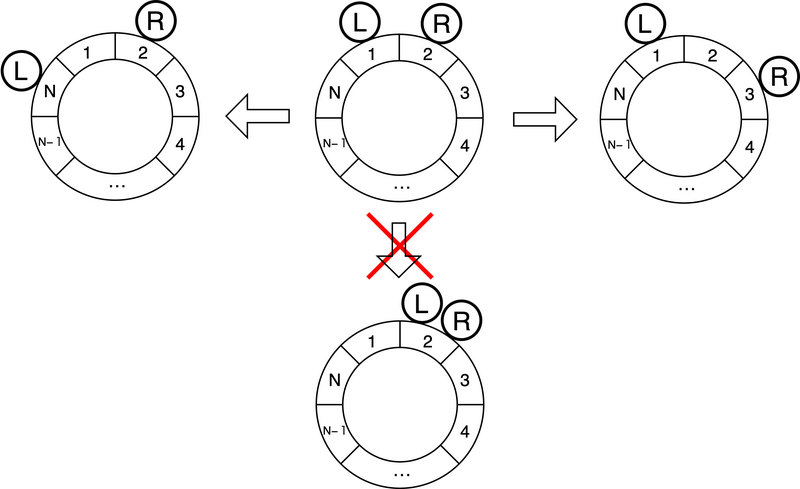
The following figure shows the initial state and examples of operations that can and cannot be made from there. The number written on each part of the ring represents the part number, and the circles labeled L and R represent your left and right hands, respectively.

You need to follow $Q$ instructions given to you in order. The $i$-th ($1 \leq i \leq Q$) instruction is represented by a character $H_i$ and an integer $T_i$, meaning the following:

• Perform some number of operations (possibly zero) so that your left hand (if $H_i$ is L) or your right hand (if $H_i$ is R) is holding part $T_i$. Here, you may move the other hand not specified by $H_i$.

Under the settings and constraints of this problem, it can be proved that any instructions are achievable.

Find the minimum total number of operations required to follow all the instructions.

The Input is given from Standard Input in the following format:

$N$ $Q$

$H_1$ $T_1$

$H_2$ $T_2$

$\vdots$

$H_Q$ $T_Q$

Print the minimum total number of operations required to follow all the instructions.

• $3\leq N \leq 3000$
• $1\leq Q \leq 3000$
• $H_i$ is L or R.
• $1 \leq T_i \leq N$
• $N$, $Q$, and $T_i$ are integers.

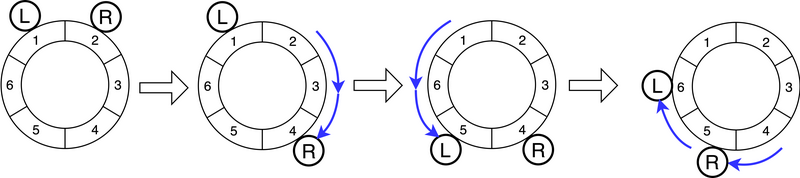
By performing the following operations, you can follow all $Q$ instructions in order.

1. Move your right hand as part $2 \rightarrow 3 \rightarrow 4$ to follow the first instruction.
2. Move your left hand as part $1 \rightarrow 6 \rightarrow 5$ to follow the second instruction.
3. Move your left hand as part $5 \rightarrow 6$, then move your right hand as part $4 \rightarrow 5$ to follow the third instruction.

In this case, the total number of operations is $2+2+1+1=6$, which is the minimum.