11234: CF1364 - D. Ehab's Last Corollary
[Creator : ]
Description
Given a connected undirected graph with $n$ vertices and an integer $k$, you have to either:
- either find an independent set that has exactly $\lceil\frac{k}{2}\rceil$ vertices.
- or find a simple cycle of length at most $k$.
An independent set is a set of vertices such that no two of them are connected by an edge. A simple cycle is a cycle that doesn't contain any vertex twice.
I have a proof that for any input you can always solve at least one of these problems, but it's left as an exercise for the reader.
- either find an independent set that has exactly $\lceil\frac{k}{2}\rceil$ vertices.
- or find a simple cycle of length at most $k$.
An independent set is a set of vertices such that no two of them are connected by an edge. A simple cycle is a cycle that doesn't contain any vertex twice.
I have a proof that for any input you can always solve at least one of these problems, but it's left as an exercise for the reader.
Input
The first line contains three integers $n$, $m$, and $k$ ($3 \le k \le n \le 10^5$, $n-1 \le m \le 2 \cdot 10^5$) — the number of vertices and edges in the graph, and the parameter $k$ from the statement.
Each of the next $m$ lines contains two integers $u$ and $v$ ($1 \le u,v \le n$) that mean there's an edge between vertices $u$ and $v$. It's guaranteed that the graph is connected and doesn't contain any self-loops or multiple edges.
Each of the next $m$ lines contains two integers $u$ and $v$ ($1 \le u,v \le n$) that mean there's an edge between vertices $u$ and $v$. It's guaranteed that the graph is connected and doesn't contain any self-loops or multiple edges.
Output
If you choose to solve the first problem, then on the first line print $1$, followed by a line containing $\lceil\frac{k}{2}\rceil$ distinct integers not exceeding $n$, the vertices in the desired independent set.
If you, however, choose to solve the second problem, then on the first line print $2$, followed by a line containing one integer, $c$, representing the length of the found cycle, followed by a line containing $c$ distinct integers not exceeding $n$, the vertices in the desired cycle, in the order they appear in the cycle.
If you, however, choose to solve the second problem, then on the first line print $2$, followed by a line containing one integer, $c$, representing the length of the found cycle, followed by a line containing $c$ distinct integers not exceeding $n$, the vertices in the desired cycle, in the order they appear in the cycle.
Sample 1 Input
4 4 3
1 2
2 3
3 4
4 1
Sample 1 Output
1
1 3
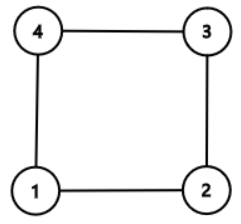
Notice that printing the independent set $\{2,4\}$ is also OK, but printing the cycle $1-2-3-4$ isn't, because its length must be at most $3$.
Sample 2 Input
4 5 3
1 2
2 3
3 4
4 1
2 4
Sample 2 Output
2
3
2 3 4
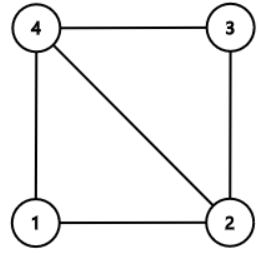
Notice that printing the independent set $\{1,3\}$ or printing the cycle $2-1-4$ is also OK.
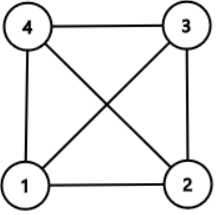
Sample 3 Input
4 6 3
1 2
2 3
3 4
4 1
1 3
2 4
Sample 3 Output
2
3
1 2 3
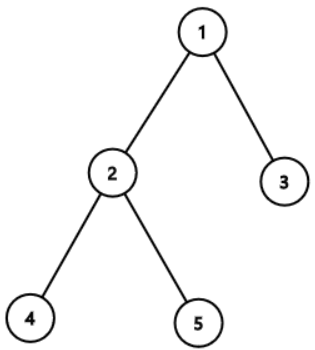
5 4 5
1 2
1 3
2 4
2 5
1
1 4 5