There are $2N$ points $P_1,P_2,\ldots,P_N, Q_1,Q_2,\ldots,Q_N$ on a two-dimensional plane. The coordinates of $P_i$ are $(A_i, B_i)$, and the coordinates of $Q_i$ are $(C_i, D_i)$. No three different points lie on the same straight line.

Determine whether there exists a permutation $R = (R_1, R_2, \ldots, R_N)$ of $(1, 2, \ldots, N)$ that satisfies the following condition. If such an $R$ exists, find one.

• For each integer $i$ from $1$ through $N$, let segment $i$ be the line segment connecting $P_i$ and $Q_{R_i}$. Then, segment $i$ and segment $j$ $(1 \leq i < j \leq N)$ never intersect.

The input is given from Standard Input in the following format:

$N$

$A_1$ $B_1$

$A_2$ $B_2$

$\vdots$

$A_N$ $B_N$

$C_1$ $D_1$

$C_2$ $D_2$

$\vdots$

$C_N$ $D_N$

If there is no $R$ satisfying the condition, print -1.

If such an $R$ exists, print $R_1, R_2, \ldots, R_N$ separated by spaces. If there are multiple solutions, you may print any of them.

• $1 \leq N \leq 300$
• $0 \leq A_i, B_i, C_i, D_i \leq 5000$ $(1 \leq i \leq N)$
• $(A_i, B_i) \neq (A_j, B_j)$ $(1 \leq i < j \leq N)$
• $(C_i, D_i) \neq (C_j, D_j)$ $(1 \leq i < j \leq N)$
• $(A_i, B_i) \neq (C_j, D_j)$ $(1 \leq i, j \leq N)$
• No three different points lie on the same straight line.
• All input values are integers.

The points are arranged as shown in the following figure.

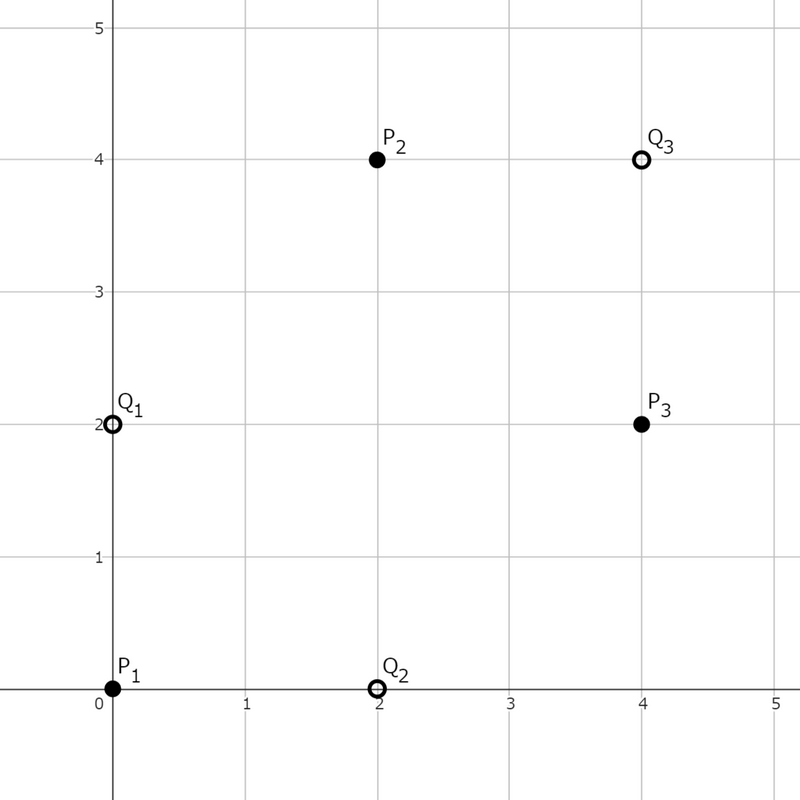
By setting $R = (2, 1, 3)$, the three line segments do not cross each other. Also, any of $R = (1, 2, 3)$, $(1, 3, 2)$, $(2, 3, 1)$, and $(3, 1, 2)$ is a valid answer.