Problem11199--ABC372 - F - Teleporting Takahashi 2

11199: ABC372 - F - Teleporting Takahashi 2

[Creator : ]
Time Limit : 1.000 sec  Memory Limit : 512 MiB

SubmitSolved: 1Submit Num: 1StatisticsShowOff!

Description

There is a simple directed graph $G$ with $N$ vertices and $N+M$ edges. The vertices are numbered $1$ to $N$, and the edges are numbered $1$ to $N+M$.

Edge $i$ $(1 \leq i \leq N)$ goes from vertex $i$ to vertex $i+1$. (Here, vertex $N+1$ is considered as vertex $1$.)
Edge $N+i$ $(1 \leq i \leq M)$ goes from vertex $X_i$ to vertex $Y_i$.

Takahashi is at vertex $1$. At each vertex, he can move to any vertex to which there is an outgoing edge from the current vertex.

Compute the number of ways he can move exactly $K$ times.

That is, find the number of integer sequences $(v_0, v_1, \dots, v_K)$ of length $K+1$ satisfying all of the following three conditions:

  • $1 \leq v_i \leq N$ for $i = 0, 1, \dots, K$.
  • $v_0 = 1$.
  • There is a directed edge from vertex $v_{i-1}$ to vertex $v_i$ for $i = 1, 2, \ldots, K$.

Since this number can be very large, print it modulo $998244353$.

Input

The input is given from Standard Input in the following format:

$N$ $M$ $K$

$X_1$ $Y_1$

$X_2$ $Y_2$

$\vdots$

$X_M$ $Y_M$

Output

Print the count modulo $998244353$.

Constraints

  • $2 \leq N \leq 2 \times 10^5$
  • $0 \leq M \leq 50$
  • $1 \leq K \leq 2 \times 10^5$
  • $1 \leq X_i, Y_i \leq N$, $X_i \neq Y_i$
  • All of the $N+M$ directed edges are distinct.
  • All input values are integers.

Sample 1 Input 

6 2 5
1 4
2 5

Sample 1 Output 

5

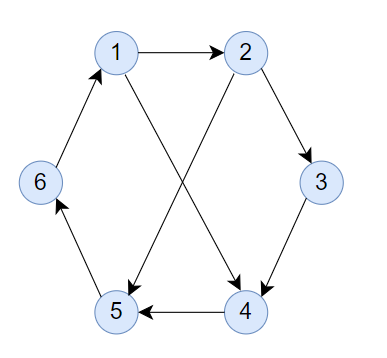
The above figure represents the graph $G$. There are five ways for Takahashi to move:

  • Vertex $1 \to$ Vertex $2 \to$ Vertex $3 \to$ Vertex $4 \to$ Vertex $5 \to$ Vertex $6$
  • Vertex $1 \to$ Vertex $2 \to$ Vertex $5 \to$ Vertex $6 \to$ Vertex $1 \to$ Vertex $2$
  • Vertex $1 \to$ Vertex $2 \to$ Vertex $5 \to$ Vertex $6 \to$ Vertex $1 \to$ Vertex $4$
  • Vertex $1 \to$ Vertex $4 \to$ Vertex $5 \to$ Vertex $6 \to$ Vertex $1 \to$ Vertex $2$
  • Vertex $1 \to$ Vertex $4 \to$ Vertex $5 \to$ Vertex $6 \to$ Vertex $1 \to$ Vertex $4$

Sample 2 Input 

10 0 200000

Sample 2 Output 

1

Sample 3 Input 

199 10 1326
122 39
142 49
164 119
197 127
188 145
69 80
6 120
24 160
18 154
185 27

Sample 3 Output 

451022766

Source/Category

 
Submit