一个 ZigZag 三元组是指一个三元组 $A_1,A_2,A_3$，满足：三个数两两不同，并且 $A_2$ 是三个数中的最大数或者最小数。
一棵节点权值为 $A_i$ 的树是 ZigZag 树，是指对于任何一个度大于 $1$ 的节点 $v$，它的任何两个相邻节点 $u,w$ 对应的 $A_u,A_v,A_w$ 是一个 ZigZag 三元组。
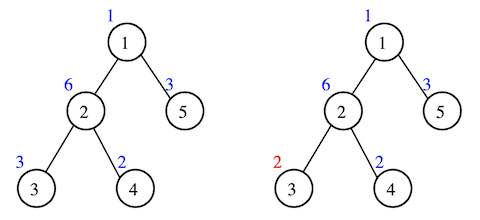
例如，下面左边的树是 ZigZag 树，因为无论如何选择 $u,v,w$，对应的 $A_u,A_v,A_w$ 都是 ZigZag 三元组；右边的树不是 ZigZag 树，因为取 $u,v,w=3,2,4$ 时 $A_u,A_v,A_w=2,6,2$ 不是 ZigZag 三元组。

对于任何一棵树 $T$，对其 ZigZag 度打分，方法如下：
1、如果 $T$ 不是 ZigZag 树，得分为 $0$。
2、如果 $T$ 是 ZigZag 树，那么得分为 $u,v,w$ 的三元组数量，其中 $v$ 是度大于 $1$ 的节点，$u,w$ 是其两个相邻的节点。注意，$u,v,w$ 和 $w,v,u$ 算同一个三元组。
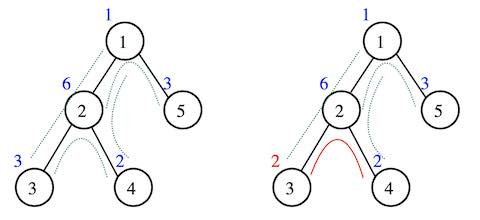
例如，下面左边的树是 ZigZag 树，有 $2,1,5$、$3,2,1$、$3,2,4$ 和 $4,2,1$ 四个三元组，ZigZag 度得分为 $4$；右边的树不是 ZigZag 树，得分为 $0$。 

小明有一棵 $N$ 个节点的树，节点权值为 $A_1,A_2,...,A_N$，小明想取其中 ZigZag 度最大的子树去参加 ZigZag 大赛。请你计算一下子树的最大 ZigZag 度。

第一行一个整数 $N$。
第二行 $N$ 个整数，依次为 $A_1,A_2,...,A_N$。
后续 $N−1$ 行，第 $i$ 行两个整数 $u_i,v_i$ 表示一条连接 $u_i$ 和 $v_i$ 的边。

一个整数，表示答案。

对于 20% 的数据，$n≤20$。
对于 12% 的数据，树是一条链。
对于 100% 的数据，$1≤N≤50000,\ 1≤A_i≤1000,\ 1≤u_i≠v_i≤N$。

4

问题描述中左侧的树。整棵树都选择的时候 ZigZag 度得分最高，为 $4$。

2

问题描述中右侧的树。去掉 3 号节点后的子树 ZigZag 度得分最高，为 2。

0

两个节点的子树理论上是 ZigZag 树，但是 ZigZag 度得分仍然是 0。