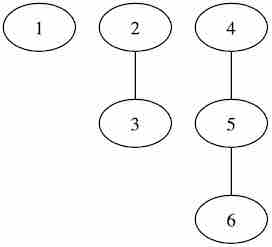
一个图是 $i−$ 和谐的，当且仅当存在一个 $i$ 个节点的连通分量。显然，一个图可以既是 $i−$ 和谐的也是 $j−$ 和谐的。例如下图，既是 1−和谐的也是 2−和谐的还是 3−和谐的，但不是 4−和谐的。

给定一个 $N$ 个节点 $M$ 条边的无向图 $G$，对于每一个 $1≤i≤N$，求在 $G$ 的基础上至少加多少条边，才能够使 $G$ 是 $i−$ 和谐的。

第一行两个整数 $N,M$，表示图 $G$ 的节点数和边数，节点编号为 $1\sim N$。
后续 $M$ 行，第 $i$ 行两个整数 $u_i,v_i$ 表示一条连接节点 $u_i$ 和 $v_i$ 的边。

输出 $N$ 行，第 $i$ 行一个整数表示在 $G$ 的基础上至少加多少条边，才能够使 $G$ 是 $i−$ 和谐的。如果无论如何都不能是 $i−$ 和谐的，输出 $−1$。

对于 20% 的数据，原图 $G$ 的连通块数量 $≤20$。
对于 40% 的数据，原图 $G$ 的连通块数量 $≤400$。
对于 100% 的数据，$1≤N≤10^5,\ 1≤M≤2×10^5,\ 1≤u_i,v_i≤N$。

0
0
0
1
1
2

$1-$ 和谐、$2−$ 和谐、$3−$ 和谐原图就有，需要加 $0$ 条边。
连接 $1$ 和 $4$ 可以得到 $4−$ 和谐；连接 $2$ 和 $4$ 可以得到 $5−$ 和谐。都只需要加 $1$ 条边。
连接 $1$ 和 $2$、$1$ 和 $4$ 可以得到 $6−$ 和谐。