There is a road extending east and west, and $N$ persons are on the road. The road extends infinitely long to the east and west from a point called the origin.

The $i$-th person $(1\leq i\leq N)$ is initially at a position $X_i$ meters east from the origin.

The persons can move along the road to the east or west. Specifically, they can perform the following movement any number of times.

• Choose one person. If there is no other person at the destination, move the chosen person $1$ meter east or west.

They have $Q$ tasks in total, and the $i$-th task $(1\leq i\leq Q)$ is as follows.

• The $T_i$-th person arrives at coordinate $G_i$.

Find the minimum total number of movements required to complete all $Q$ tasks in order.

The input is given from Standard Input in the following format:

$N$

$X_1$ $X_2$ $\ldots$ $X_N$

$Q$

$T_1$ $G_1$

$T_2$ $G_2$

$\vdots$

$T_Q$ $G_Q$

• $1\leq N\leq2\times10^5$
• $0\leq X_1 < X_2 < \dotsb < X_N \leq10^8$
• $1\leq Q\leq2\times10^5$
• $1\leq T_i\leq N\ (1\leq i\leq Q)$
• $0\leq G_i\leq10^8\ (1\leq i\leq Q)$
• All input values are integers.

An optimal sequence of movements for the persons is as follows (the positions of the persons are not necessarily drawn to scale):

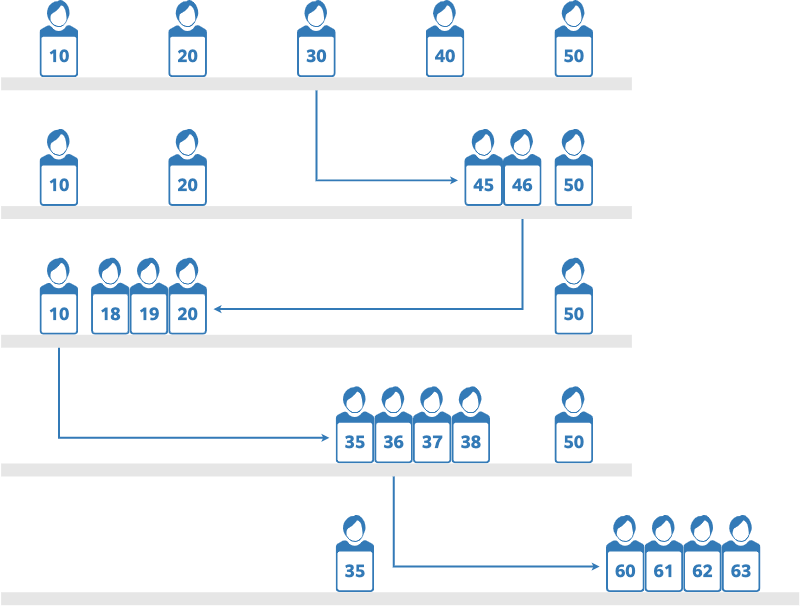
For each task, the persons move as follows.

• The 4th person moves $6$ steps east, and the 3rd person moves $15$ steps east.
• The 2nd person moves $2$ steps west, the 3rd person moves $26$ steps west, and the 4th person moves $26$ steps west.
• The 4th person moves $18$ steps east, the 3rd person moves $18$ steps east, the 2nd person moves $18$ steps east, and the 1st person moves $25$ steps east.
• The 5th person moves $13$ steps east, the 4th person moves $24$ steps east, the 3rd person moves $24$ steps east, and the 2nd person moves $24$ steps east.

The total number of movements is $21+54+79+85=239$.

You cannot complete all tasks with a total movement count of $238$ or less, so print 239.

Note that some persons may need to move to the west of the origin or more than $10^8$ meters to the east of it.

Also, note that the answer may exceed $2^{32}$.