You are given simple undirected graphs $G$ and $H$, each with $N$ vertices: vertices $1$, $2$, $\ldots$, $N$. Graph $G$ has $M_G$ edges, and its $i$-th edge $(1\leq i\leq M_G)$ connects vertices $u_i$ and $v_i$. Graph $H$ has $M_H$ edges, and its $i$-th edge $(1\leq i\leq M_H)$ connects vertices $a_i$ and $b_i$.
You can perform the following operation on graph $H$ any number of times, possibly zero.

• Choose a pair of integers $(i,j)$ satisfying $1\leq i<j\leq N$. Pay $A_{i,j}$ yen, and if there is no edge between vertices $i$ and $j$ in $H$, add one; if there is, remove it.

Find the minimum total cost required to make $G$ and $H$ isomorphic.

>>>What is a simple undirected graph?<<<

A simple undirected graph is a graph without self-loops or multi-edges, where edges have no direction.

>>>What does it mean for graphs to be isomorphic?<<<

Two graphs $G$ and $H$ with $N$ vertices are isomorphic if and only if there exists a permutation $(P_1,P_2,\ldots,P_N)$ of $(1,2,\ldots,N)$ such that for all $1\leq i\lt j\leq N$:

• an edge exists between vertices $i$ and $j$ in $G$ if and only if an edge exists between vertices $P_i$ and $P_j$ in $H$.

The input is given from Standard Input in the following format:
$N$
$M _ G$
$u _ 1$ $v _ 1$
$u _ 2$ $v _ 2$
$\vdots$
$u _ {M _ G}$ $v _ {M _ G}$
$M _ H$
$a _ 1$ $b _ 1$
$a _ 2$ $b _ 2$
$\vdots$
$a _ {M _ H}$ $b _ {M _ H}$
$A _ {1,2}$ $A _ {1,3}$ $\ldots$ $A _ {1,N}$
$A _ {2,3}$ $\ldots$ $A _ {2,N}$
$\vdots$
$A _ {N-1,N}$

Print the answer.

• $1\leq N\leq8$
• $0\leq M _ G\leq\dfrac{N(N-1)}2$
• $0\leq M _ H\leq\dfrac{N(N-1)}2$
• $1\leq u _ i\lt v _ i\leq N\ (1\leq i\leq M _ G)$
• $(u _ i,v _ i)\neq(u _ j,v _ j)\ (1\leq i\lt j\leq M _ G)$
• $1\leq a _ i\lt b _ i\leq N\ (1\leq i\leq M _ H)$
• $(a _ i,b _ i)\neq(a _ j,b _ j)\ (1\leq i\lt j\leq M _ H)$
• $1\leq A _ {i,j}\leq 10 ^ 6\ (1\leq i\lt j\leq N)$
• All input values are integers.

9

The given graphs are as follows:

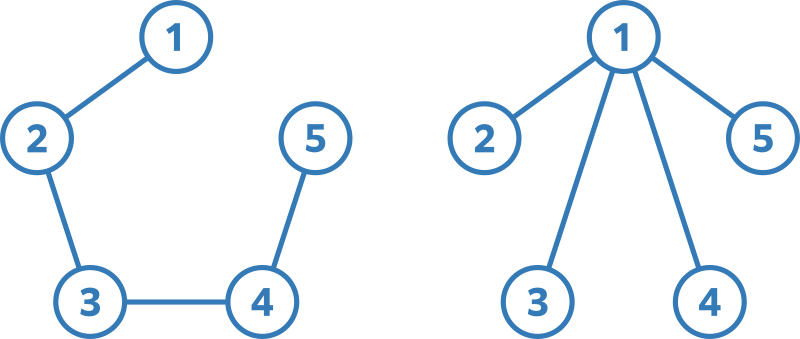
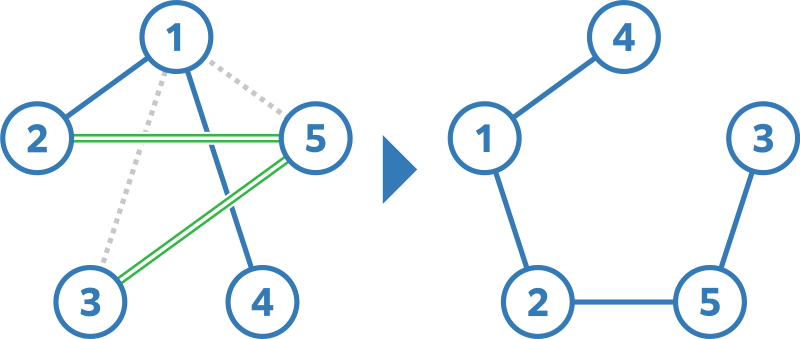
For example, you can perform the following four operations on $H$ to make it isomorphic to $G$ at a cost of $9$ yen.

• Choose $(i,j)=(1,3)$. There is an edge between vertices $1$ and $3$ in $H$, so pay $1$ yen to remove it.
• Choose $(i,j)=(2,5)$. There is no edge between vertices $2$ and $5$ in $H$, so pay $2$ yen to add it.
• Choose $(i,j)=(1,5)$. There is an edge between vertices $1$ and $5$ in $H$, so pay $1$ yen to remove it.
• Choose $(i,j)=(3,5)$. There is no edge between vertices $3$ and $5$ in $H$, so pay $5$ yen to add it.

After these operations, $H$ becomes:

You cannot make $G$ and $H$ isomorphic at a cost less than $9$ yen, so print 9.

3

For example, performing the operations $(i,j)=(2,3),(2,4),(3,4)$ on $H$ will make it isomorphic to $G$.

5

For example, performing the operation $(i,j)=(4,5)$ once will make $G$ and $H$ isomorphic.

0

Note that $G$ and $H$ may have no edges.
Also, it is possible that no operations are needed.