There is a grid with $H$ rows and $W$ columns. Let $(i,j)$ denote the cell at the $i$-th row from the top and $j$-th column from the left.

There are $N$ coins on this grid, and the $i$-th coin can be picked up by passing through the cell $(R_i,C_i)$.

Your goal is to start from cell $(1,1)$, repeatedly move either down or right by one cell, and reach cell $(H,W)$ while picking up as many coins as possible.

Find the maximum number of coins you can pick up and one of the paths that achieves this maximum.

The input is given from Standard Input in the following format:

$H$ $W$ $N$

$R_1$ $C_1$

$R_2$ $C_2$

$\vdots$

$R_N$ $C_N$

Print two lines. The first line should contain the maximum number of coins you can pick up. The second line should contain one of the paths that achieves this maximum as a string of length $H+W-2$. The $i$-th character of this string should be D if the $i$-th move is downward, and R if it is rightward.

If there are multiple paths that maximize the number of coins picked up, you may print any of them.

• $2\leq H,W \leq 2\times 10^5$
• $1\leq N \leq \min(HW-2, 2\times 10^5)$
• $1\leq R_i \leq H$
• $1\leq C_i \leq W$
• $(R_i,C_i)\neq (1,1)$
• $(R_i,C_i)\neq (H,W)$
• $(R_i,C_i)$ are pairwise distinct.
• All input values are integers.

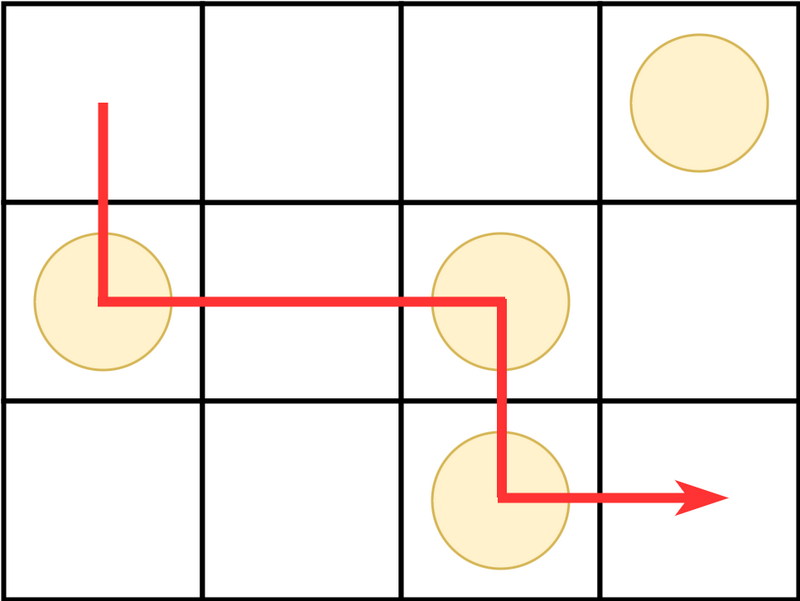
As shown in the figure above, by moving $(1,1)\rightarrow (2,1)\rightarrow (2,2)\rightarrow (2,3)\rightarrow (3,3)\rightarrow (3,4)$, you can pick up three coins at $(2,1),(2,3),(3,3)$.

The path RD is also acceptable.