11135: ABC368 - D - Minimum Steiner Tree
[Creator : ]
Description
You are given a tree with $N$ vertices numbered $1$ to $N$. The $i$-th edge connects vertices $A_i$ and $B_i$.
Consider a tree that can be obtained by removing some (possibly zero) edges and vertices from this graph. Find the minimum number of vertices in such a tree that includes all of $K$ specified vertices $V_1,\ldots,V_K$.
Input
The input is given from Standard Input in the following format:
$N$ $K$
$A_1$ $B_1$
$\vdots$
$A_{N-1}$ $B_{N-1}$
$V_1$ $\ldots$ $V_K$
Output
Print the answer.
Constraints
- $1 \leq K \leq N \leq 2\times 10^5$
- $1 \leq A_i,B_i \leq N$
- $1 \leq V_1 < V_2 < \ldots < V_K \leq N$
- The given graph is a tree.
- All input values are integers.
Sample 1 Input
7 3
1 2
1 3
2 4
2 5
3 6
3 7
1 3 5
Sample 1 Output
4
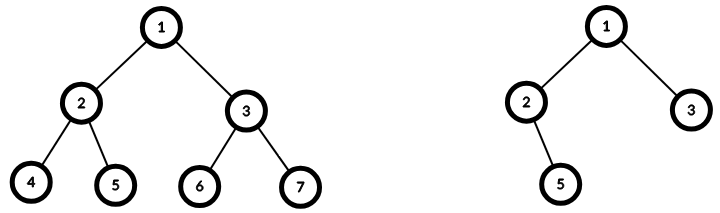
The given tree is shown on the left in the figure below. The tree with the minimum number of vertices that includes all of vertices $1,3,5$ is shown on the right.
Sample 2 Input
4 4
3 1
1 4
2 1
1 2 3 4
Sample 2 Output
4
Sample 3 Input
5 1
1 4
2 3
5 2
1 2
1
Sample 3 Output
1