11073: 学习系列 —— 无旋平衡树之 FHQ Treap
Description
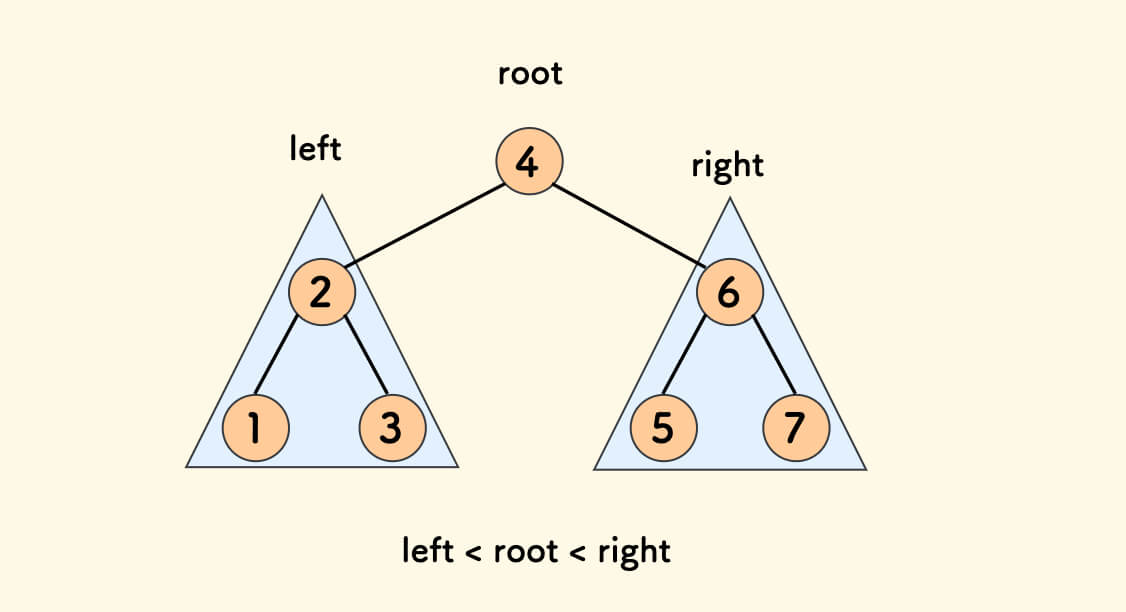
二叉搜索树 BST
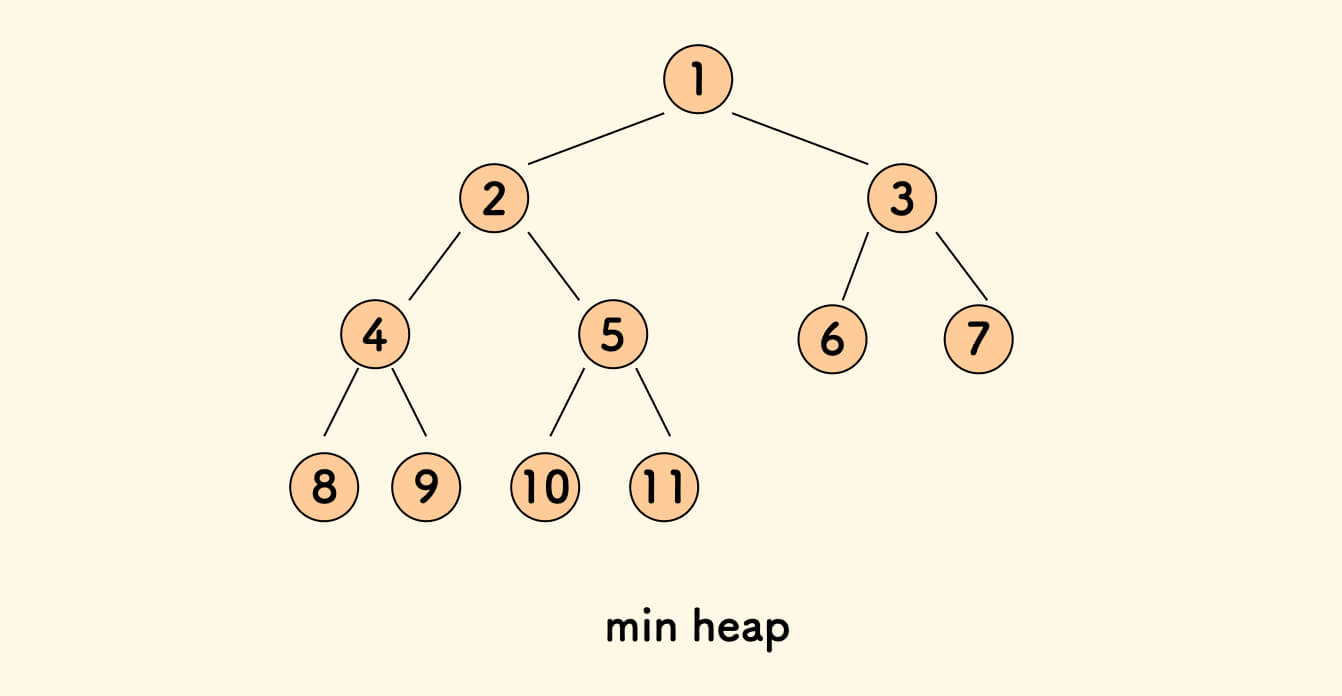
堆 Heap
树堆 Treap
树堆(Treap)= 二叉搜索树(BST)+ 堆(Heap)。
树堆的节点维护两个信息:
权值 val - 按此值形成 BST
随机值 rnd - 按此值形成 Heap,以实现随机平衡(弱平衡)。
FHQ Treap 是一种最常用的无旋 Treap,核心操作只有两个:
分裂:按权值 val 分裂,递归过程。
合并:按随机值 rnd 合并,递归过程。
Input
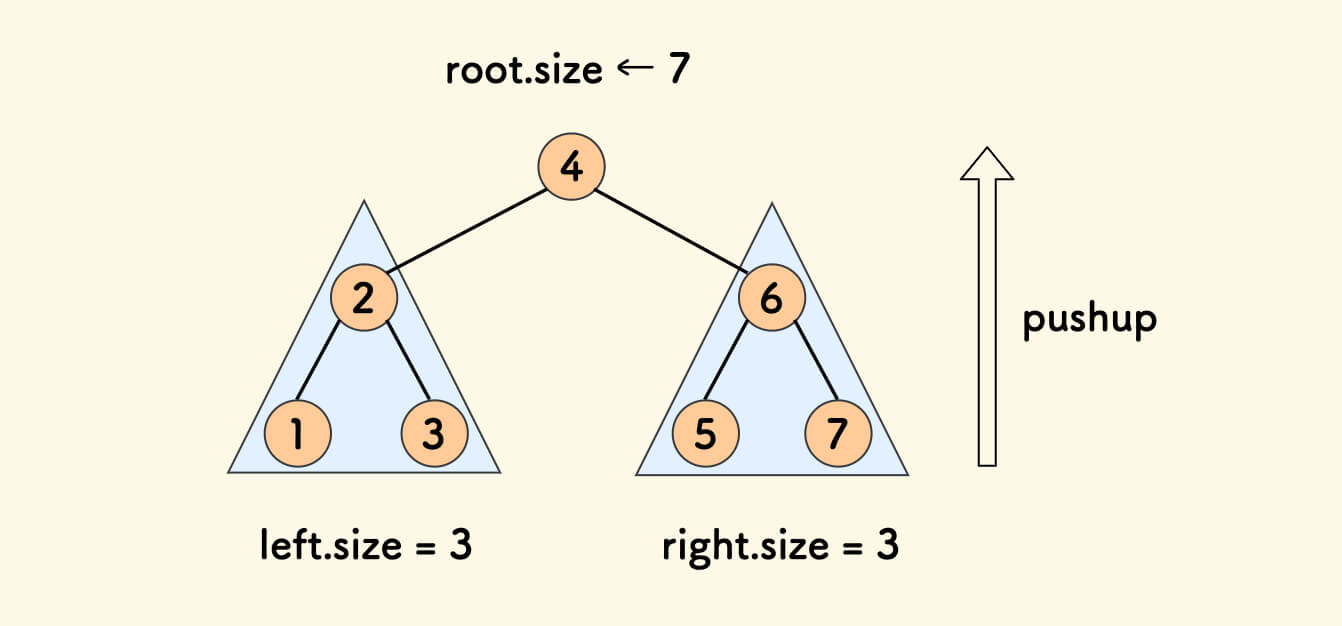
pushup
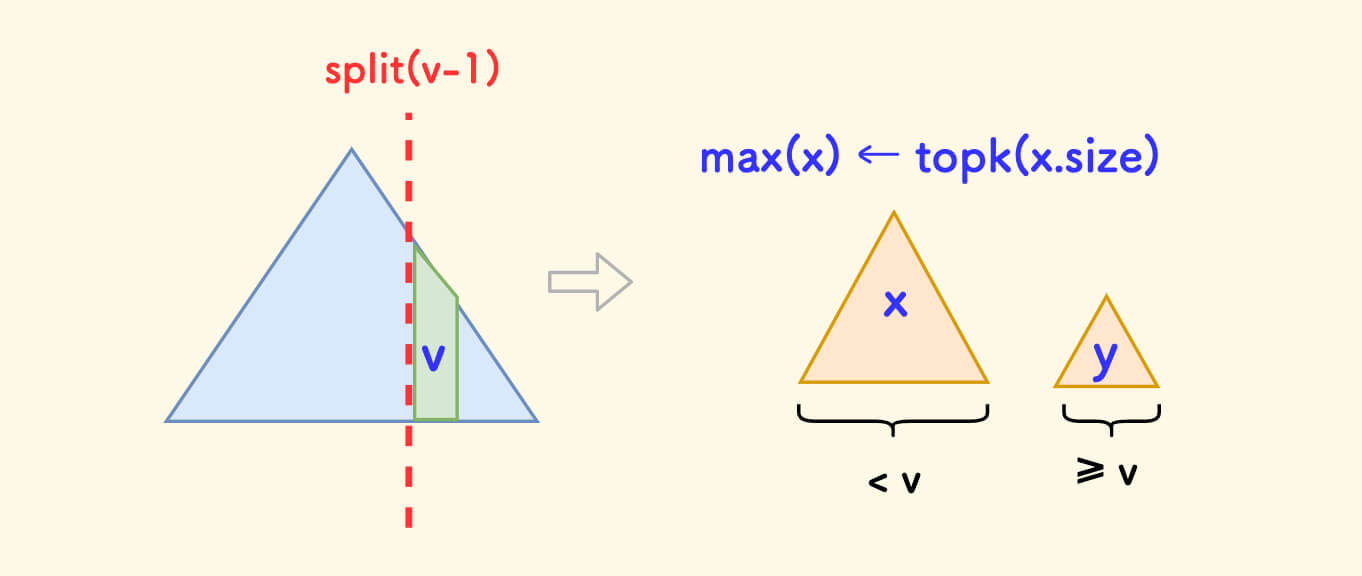
分裂 Split
分裂函数 split(p, v, &x, &y) 的含义是:
把树 p 按值 v 分裂成两颗子树:左边的 x 和 右边的 y。
使得分裂后子树 x 中的权值全部不大于 v,子树 y 中的权值全部大于 v。

显然,分裂后的两颗子树也是 treap。
分裂操作的动态示意图如下:
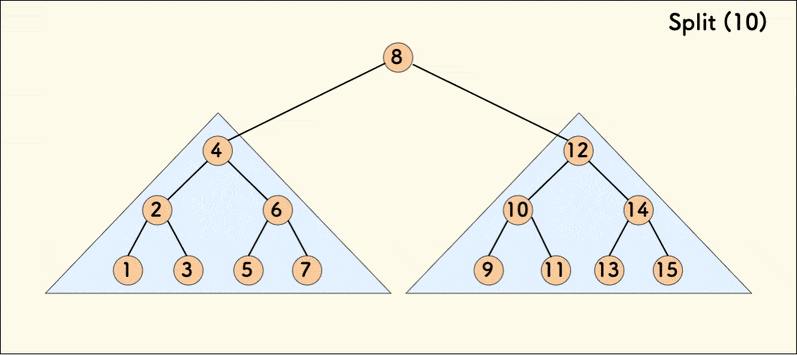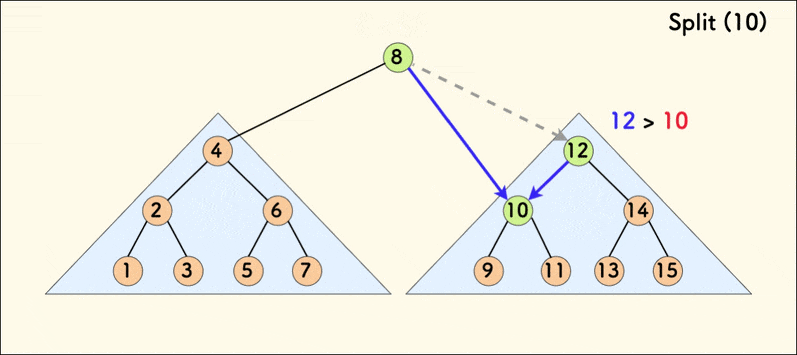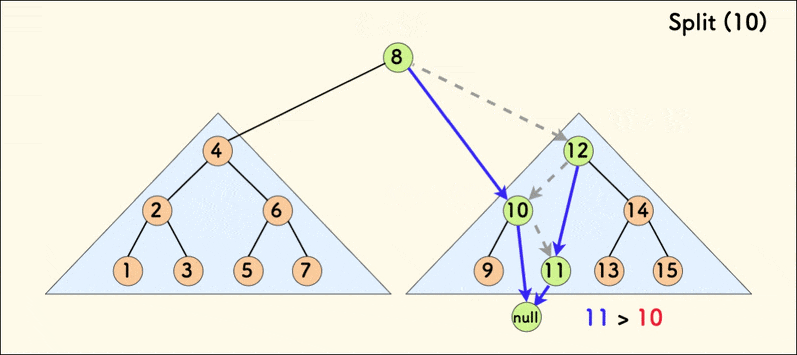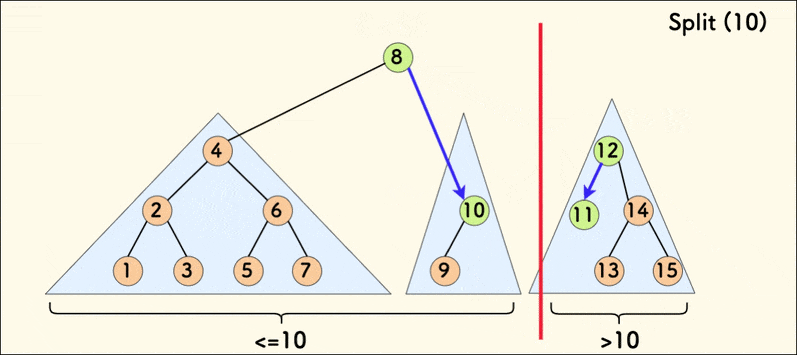
在树相对平衡的情况下,分裂的平均时间复杂度是 $O(logn)$。
可以看到,分裂操作只利用了二叉搜索树的性质。
一个重要的性质是,分裂不改变中序遍历。详细点说是,分裂不会改变任意两个节点在中序遍历中位置的相对顺序。
在下图中,中序遍历的结果可以映射到一根数轴上,可以看到分裂并不影响中序。
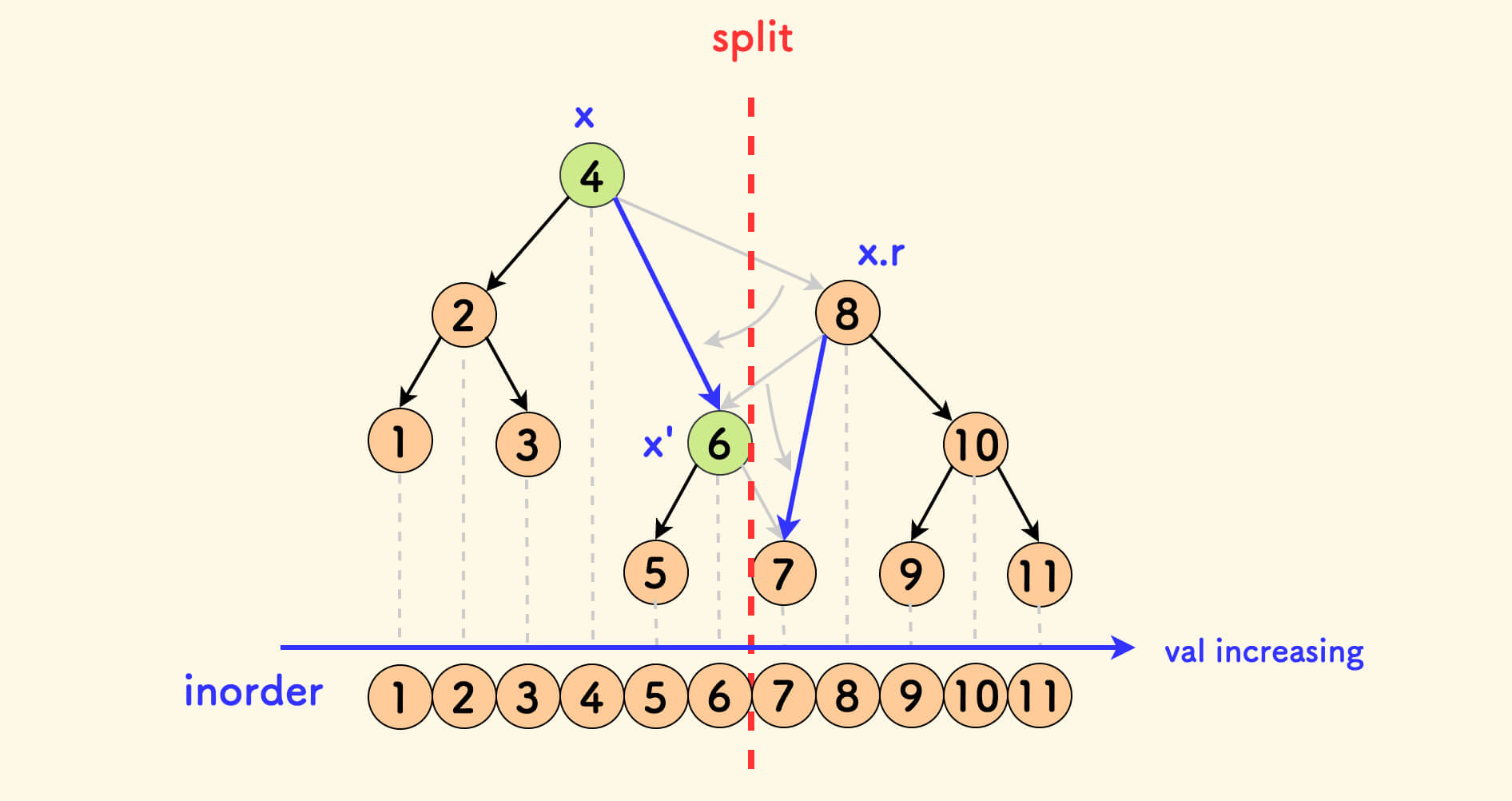
Output
合并
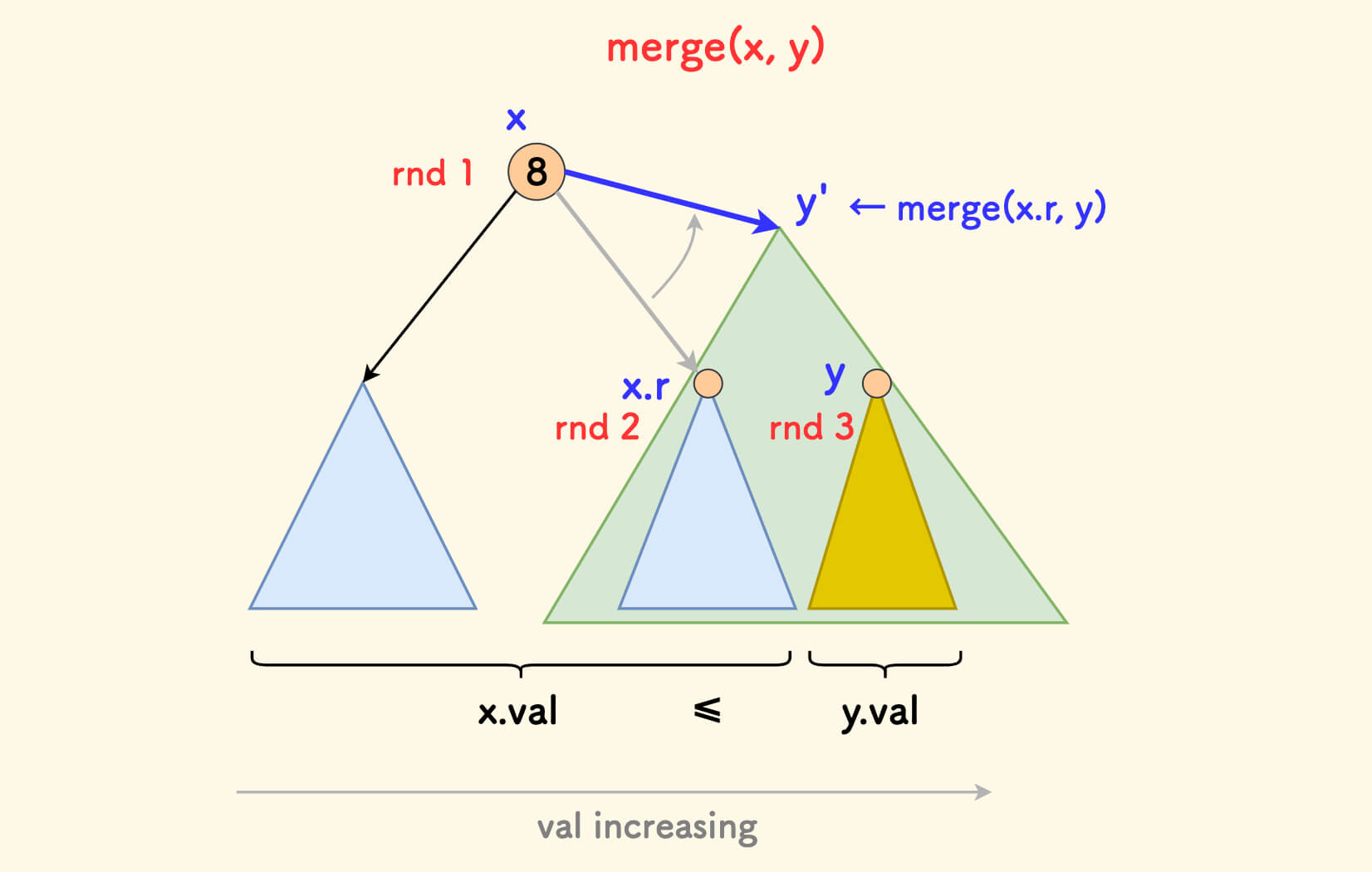
合并操作的动态示意图如下:
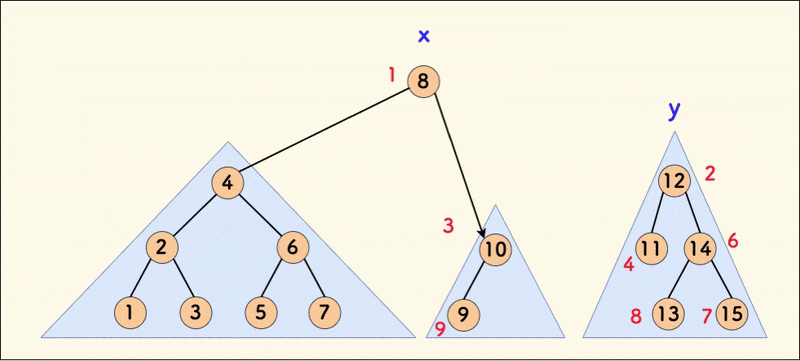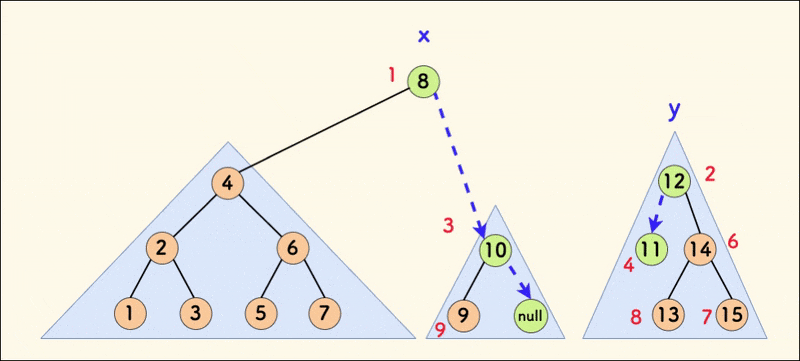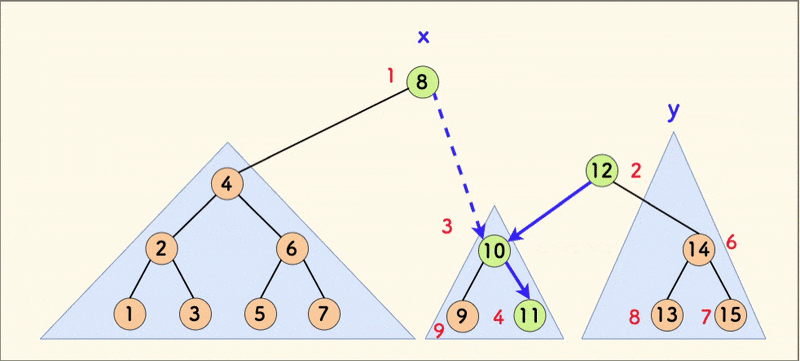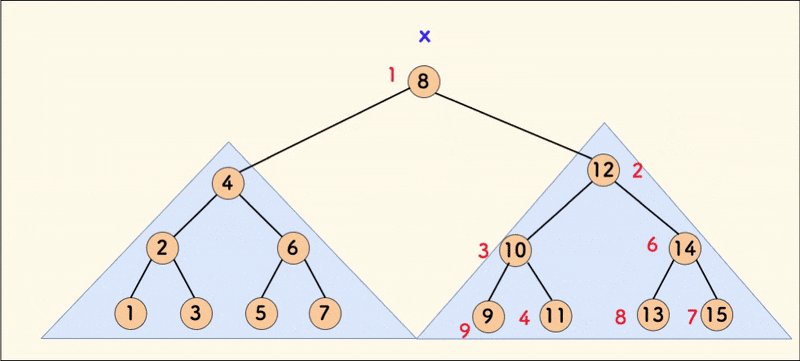
在树相对平衡的情况下,合并的平均时间复杂度是 $O(logn)$。
可以看到,合并操作保障了堆的性质,进而让 treap 平衡(绝大多数情况下)。
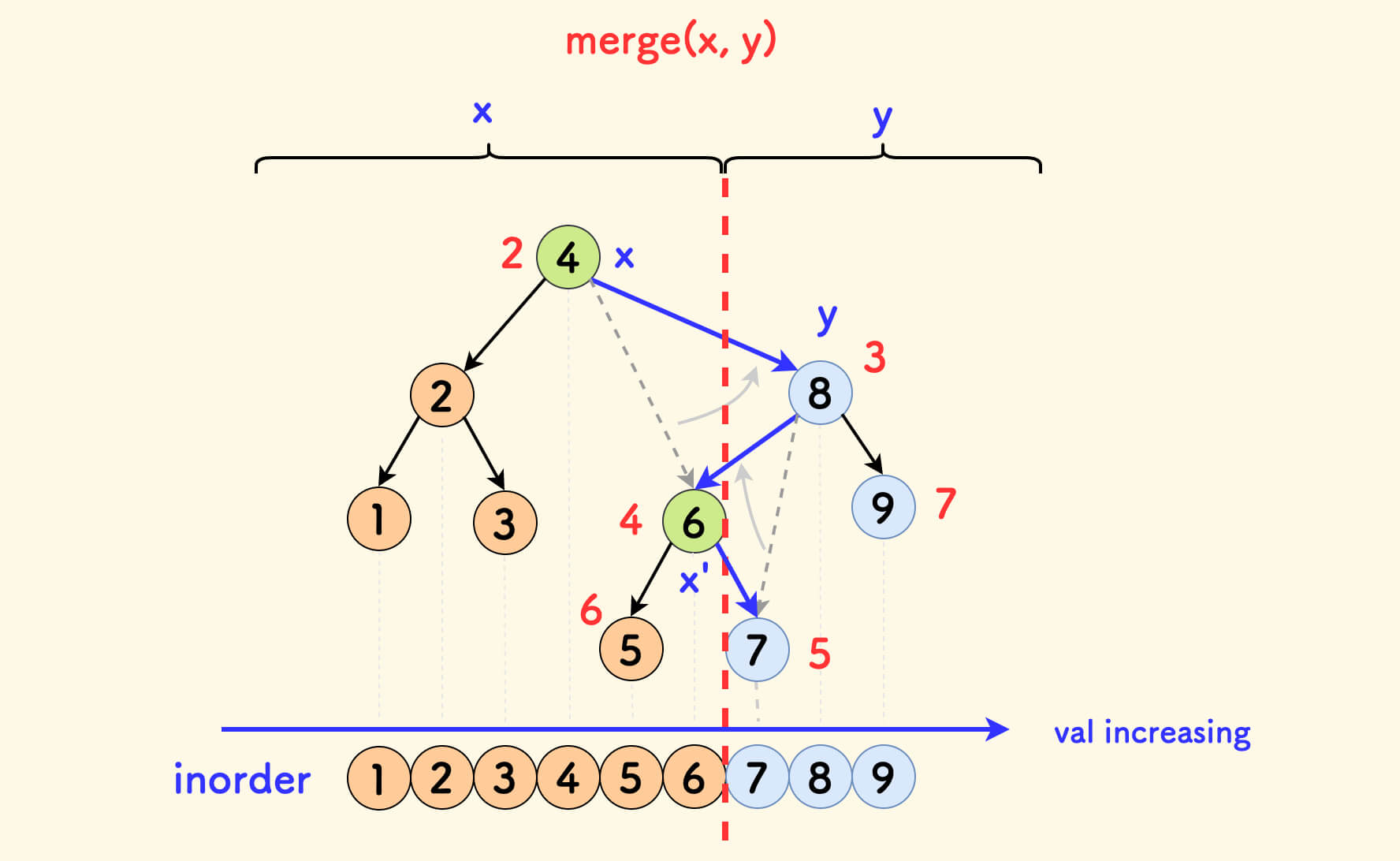
同样,一个重要的性质是,合并不改变中序遍历。
下图中,中序遍历的结果映射到一根数轴上,在满足 x 的权值全部不大于 y 的权值的情况下, 合并操作并不影响中序(其中,节点旁边的红色数字是随机值)。
Constraints
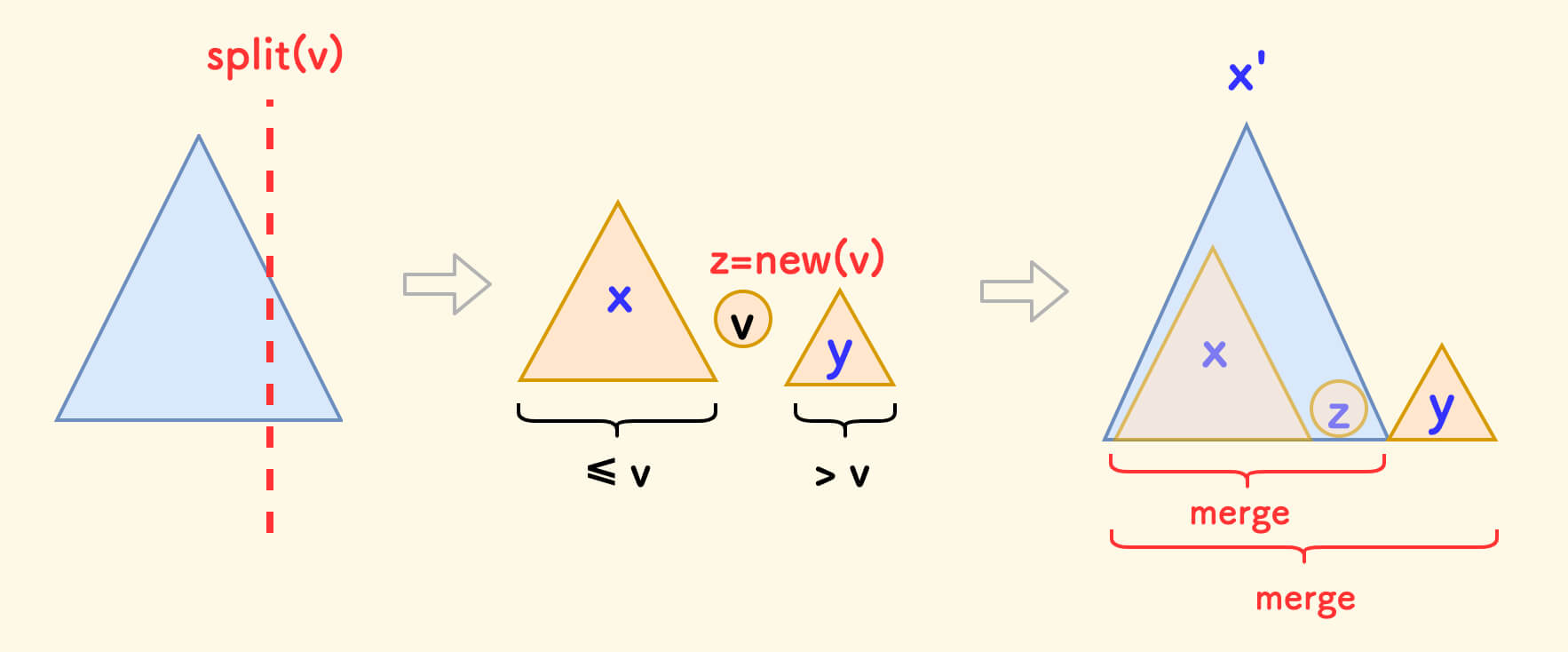
删除
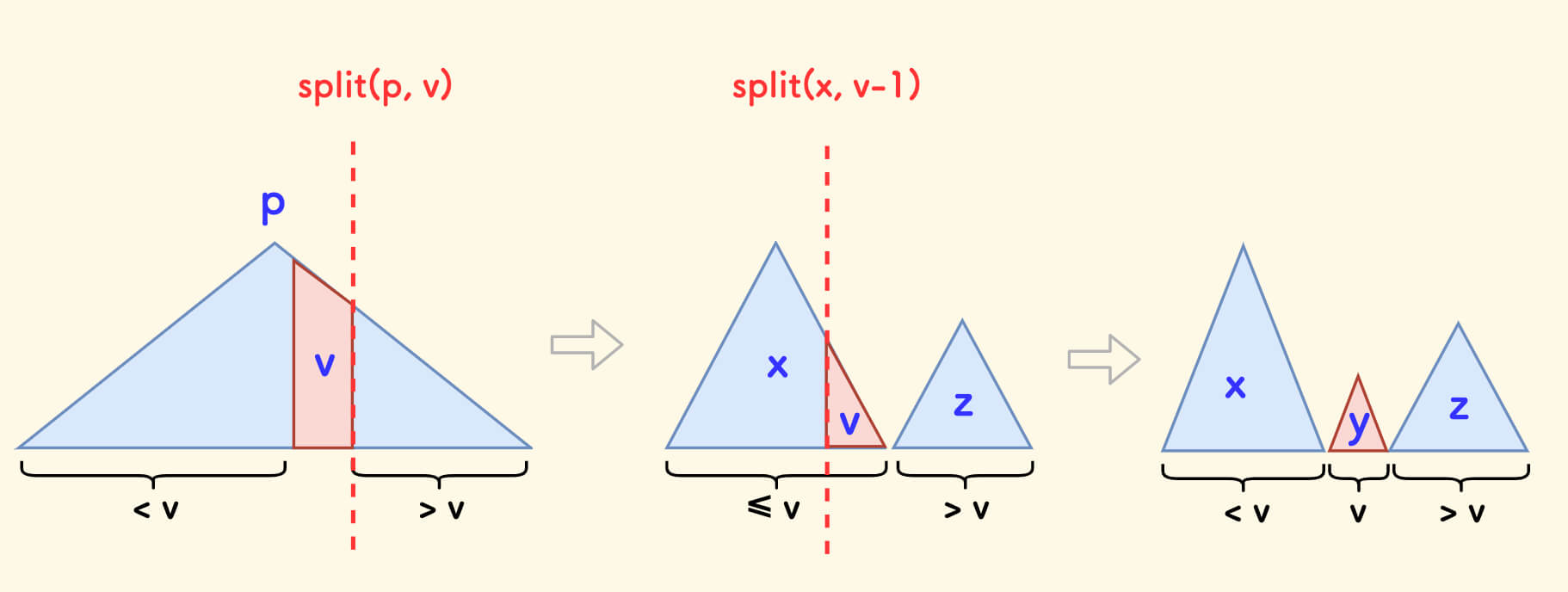
排名 Rank
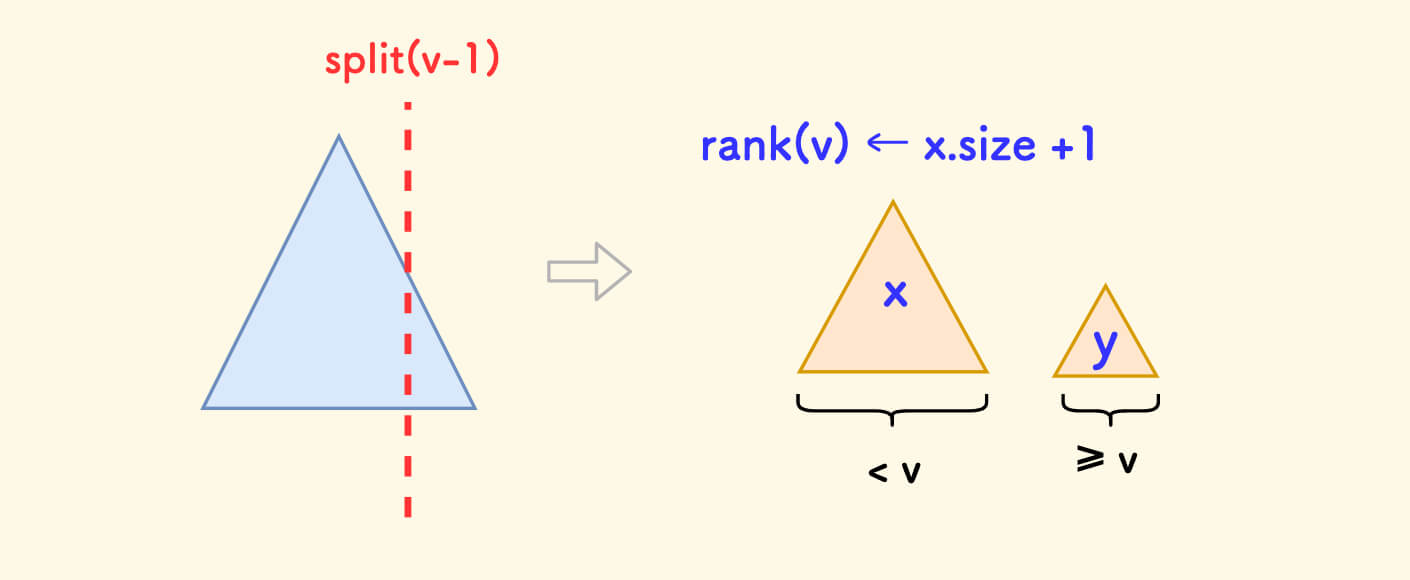
第 K 小
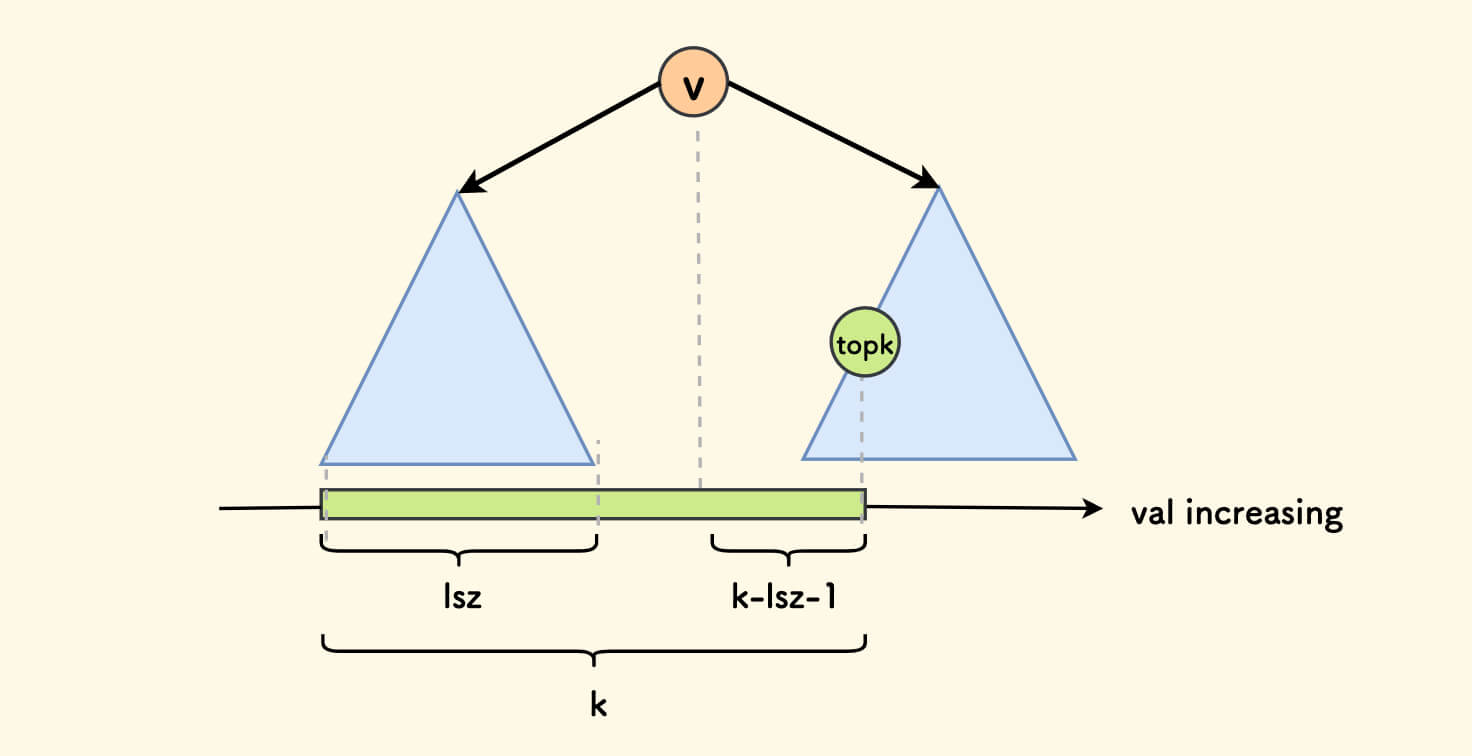
前驱,后继