11036: 洛谷P10997 - Partition
[Creator : ]
Description
你有 $n$ 行 $m$ 列的一个矩阵,第 $i$ 行第 $j$ 列的格子(记作 $(i,j)$)上写有一个整数 $a_{i,j}$。
- 称 $(a,b)$ 在 $(c,d)$ 的下方,当且仅当 $b=d,a>c$,即同一列中,行编号更大。
- 称 $(a,b)$ 在 $(c,d)$ 的上方,当且仅当 $(c,d)$ 在 $(a,b)$ 的下方。
- 称 $(a,b)$ 在 $(c,d)$ 的右边,当且仅当 $a=c,b>d$,即同一行中,列编号更大。
- 称 $(a,b)$ 在 $(c,d)$ 的左边,当且仅当 $(c,d)$ 在 $(a,b)$ 的右边。
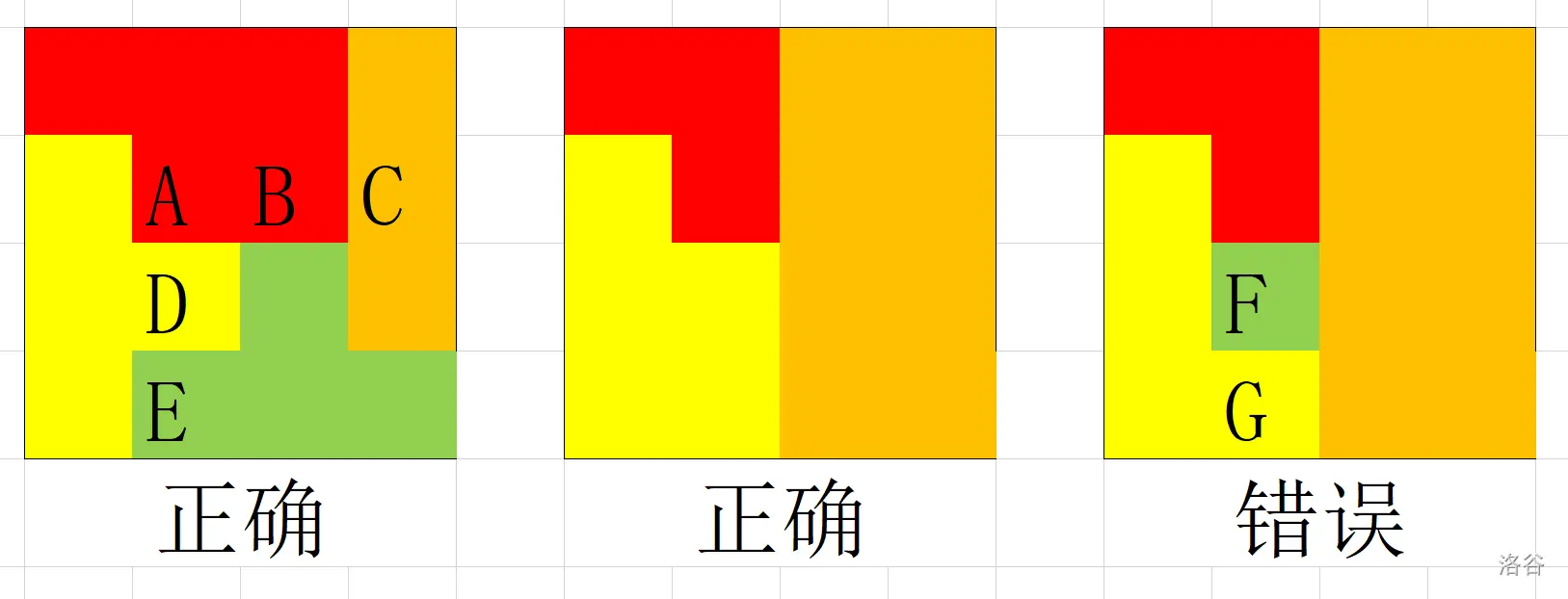
如图,$A(2,2)$ 下方有 $D(3,2),E(4,2)$,右边有 $B(2,3),C(2,4)$。
为了让矩阵更加美观,你想要给每个格子涂上红、橙、黄、绿四种颜色之一,有很多种方案,但是如果一个方案满足如下要求,就称这个方案是简单的:
- 红色格子的上方只能是红色格子,左边只能是红色或黄色格子,右边只能是红色或橙色格子。
- 橙色格子的右边只能是橙色格子,上方只能是橙色或红色格子,下方只能是橙色或绿色格子。
- 绿色格子的下方只能是绿色格子,右边只能是绿色或橙色格子,左边只能是绿色或黄色格子。
- 黄色格子的左边只能是黄色格子,下方只能是黄色或绿色格子,上方只能是黄色或红色格子。
上图中展示了一些可能的染色方案,其中:
- 第一幅图是简单的。
- 第二幅图也是简单的。注意如果一种颜色的格子不存在,那么可以直接忽略对应要求。
- 第三幅图不是简单的,因为 $F(3,2)$ 绿色格子下方有 $G(4,2)$ 是黄色,不符合第四条要求。
若 $(i,j)$ 的颜色为红、橙、黄、绿,则这个格子的权值 $w_{i,j}$ 分别为 $1,2,3,4$。计算所有简单的方案中,$\sum\limits_{i=1}^n\sum\limits_{j=1}^m a_{i,j} w_{i,j}$ 的最大值。
- 称 $(a,b)$ 在 $(c,d)$ 的下方,当且仅当 $b=d,a>c$,即同一列中,行编号更大。
- 称 $(a,b)$ 在 $(c,d)$ 的上方,当且仅当 $(c,d)$ 在 $(a,b)$ 的下方。
- 称 $(a,b)$ 在 $(c,d)$ 的右边,当且仅当 $a=c,b>d$,即同一行中,列编号更大。
- 称 $(a,b)$ 在 $(c,d)$ 的左边,当且仅当 $(c,d)$ 在 $(a,b)$ 的右边。
如图,$A(2,2)$ 下方有 $D(3,2),E(4,2)$,右边有 $B(2,3),C(2,4)$。

为了让矩阵更加美观,你想要给每个格子涂上红、橙、黄、绿四种颜色之一,有很多种方案,但是如果一个方案满足如下要求,就称这个方案是简单的:
- 红色格子的上方只能是红色格子,左边只能是红色或黄色格子,右边只能是红色或橙色格子。
- 橙色格子的右边只能是橙色格子,上方只能是橙色或红色格子,下方只能是橙色或绿色格子。
- 绿色格子的下方只能是绿色格子,右边只能是绿色或橙色格子,左边只能是绿色或黄色格子。
- 黄色格子的左边只能是黄色格子,下方只能是黄色或绿色格子,上方只能是黄色或红色格子。
上图中展示了一些可能的染色方案,其中:
- 第一幅图是简单的。
- 第二幅图也是简单的。注意如果一种颜色的格子不存在,那么可以直接忽略对应要求。
- 第三幅图不是简单的,因为 $F(3,2)$ 绿色格子下方有 $G(4,2)$ 是黄色,不符合第四条要求。
若 $(i,j)$ 的颜色为红、橙、黄、绿,则这个格子的权值 $w_{i,j}$ 分别为 $1,2,3,4$。计算所有简单的方案中,$\sum\limits_{i=1}^n\sum\limits_{j=1}^m a_{i,j} w_{i,j}$ 的最大值。
Input
输入的第一行是两个正整数 $n,m$,表示矩阵的行数和列数。
之后有 $n$ 行,每行 $m$ 个整数。第 $i$ 行第 $j$ 个整数表示 $a_{i,j}$。
之后有 $n$ 行,每行 $m$ 个整数。第 $i$ 行第 $j$ 个整数表示 $a_{i,j}$。
Output
输出一行一个整数表示答案。
Constraints
对于全体数据,保证 $1\le n,m\le 2000$,$|a_{i,j}|\le 10^9$。
Sample 1 Input
3 4
8 -2 -5 7
-4 6 -1 -3
5 1 4 3
Sample 1 Output
87

染色方案如上图所示。
Sample 2 Input
10 10
-607544439 -979004727 -312554064 -699869702 666983975 -320873934 -942207367 -178682386 275703899 -502153774
410971617 -76369893 -359278237 275932972 -86448038 714539457 -54215653 -250390633 -543539625 929531007
718862112 -158262990 482471050 -836696543 791951750 239968249 -766605973 -759094194 -19007257 907151693
-348361375 170949857 -285590070 402599195 469840858 288238039 410877678 179198841 60474475 813298551
-49654250 -340449178 -818518909 981342312 -472457171 144738808 -78496024 119951006 719889194 589539617
-343916789 -102845130 647967162 178223670 -520096558 -701610878 769986590 -306817394 776077393 891533714
-652884066 743855180 513738054 837511580 -206701878 751808326 -442751338 507912998 -51199158 -548890634
-19583239 -517604006 -564570564 -853892671 738975088 851320757 -595055422 852889648 213674342 -548020267
779798717 -323958612 577597457 -318242425 57184511 189209789 347708858 891010501 322410555 -669564400
623568486 123756685 -925342948 -864544839 -83746874 680094424 335536285 -977426931 -724040964 -337707402
Sample 2 Output
26663074561