11030: CF1823 - F. Random Walk
[Creator : ]
Description
You are given a tree consisting of $n$ vertices and $n−1$ edges, and each vertex $v$ has a counter $c(v)$ assigned to it.
Initially, there is a chip placed at vertex $s$ and all counters, except $c(s)$, are set to $0$; $c(s)$ is set to $1$.
Your goal is to place the chip at vertex $t$. You can achieve it by a series of moves. Suppose right now the chip is placed at the vertex $v$. In one move, you do the following:
For each vertex $v$ calculate the expected value of $c(v)$ modulo $998244353$.
Initially, there is a chip placed at vertex $s$ and all counters, except $c(s)$, are set to $0$; $c(s)$ is set to $1$.
Your goal is to place the chip at vertex $t$. You can achieve it by a series of moves. Suppose right now the chip is placed at the vertex $v$. In one move, you do the following:
- choose one of neighbors $to$ of vertex $v$ uniformly at random ($to$ is neighbor of $v$ if and only if there is an edge $\{v,to\}$ in the tree);
- move the chip to vertex $to$ and increase $c(to)$ by $1$;
For each vertex $v$ calculate the expected value of $c(v)$ modulo $998244353$.
Input
The first line contains three integers $n, s, t\ (2≤n≤2⋅10^5;\ 1≤s,t≤n;\ s≠t)$ — number of vertices in the tree and the starting and finishing vertices.
Next $n−1$ lines contain edges of the tree: one edge per line. The $i$-th line contains two integers $u_i, v_i\ (1≤u_i,v_i≤n;\ u_i≠v_i)$, denoting the edge between the nodes $u_i$ and $v_i$.
It's guaranteed that the given edges form a tree.
Next $n−1$ lines contain edges of the tree: one edge per line. The $i$-th line contains two integers $u_i, v_i\ (1≤u_i,v_i≤n;\ u_i≠v_i)$, denoting the edge between the nodes $u_i$ and $v_i$.
It's guaranteed that the given edges form a tree.
Output
Print nn numbers: expected values of $c(v)$ modulo $998244353$ for each $v$ from $1$ to $n$.
Formally, let $M=998244353$. It can be shown that the answer can be expressed as an irreducible fraction $\frac{p}{q}$, where $p$ and $q$ are integers and $q≢0\ (\bmod\ M)$. Output the integer equal to $p⋅q^{−1}\bmod\ M$. In other words, output such an integer $x$ that $0≤x<M$ and $x⋅q≡p(\bmod\ M)$.
Formally, let $M=998244353$. It can be shown that the answer can be expressed as an irreducible fraction $\frac{p}{q}$, where $p$ and $q$ are integers and $q≢0\ (\bmod\ M)$. Output the integer equal to $p⋅q^{−1}\bmod\ M$. In other words, output such an integer $x$ that $0≤x<M$ and $x⋅q≡p(\bmod\ M)$.
Sample 1 Input
3 1 3
1 2
2 3
Sample 1 Output
2 2 1
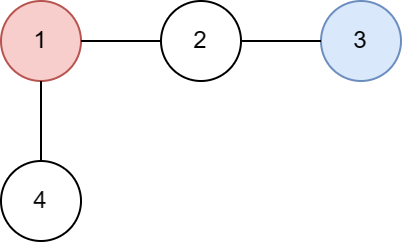
The tree from this example is shown below:

Let's calculate expected value $E[c(1)]$:

Let's calculate expected value $E[c(1)]$:
- $P(c(1)=0)=0$, since $c(1)$ is set to $1$ from the start.
- $P(c(1)=1)=\frac{1}{2}$, since there is the only one series of moves that leads $c(1)=1$. It's $1→2→3$ with probability $1⋅\frac{1}{2}$.
- $P(c(1)=2)=\frac{1}{4}$: the only path is $1→_12→_{0.5}1→_12→_{0.5}3$.
- $P(c(1)=3)=\frac{1}{8}$: the only path is $1→_12→_{0.5}1→_12→_{0.5}1→_12→_{0.5}3$.
- $P(c(1)=i)=\frac{1}{2^i}$ in general case.
Sample 2 Input
4 1 3
1 2
2 3
1 4
Sample 2 Output
4 2 1 2
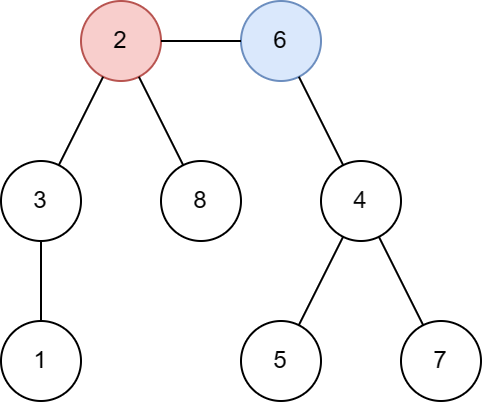
Sample 3 Input
8 2 6
6 4
6 2
5 4
3 1
2 3
7 4
8 2
Sample 3 Output
1 3 2 0 0 1 0 1