10981: 换位思考
[Creator : ]
Description
小 Y 觉得自己不会换位思考,于是他去向换位大师请教。
于是,换位大师给小 Y 出了这样一个题:
但是小 Y 还是不会换位思考,所以他来问你了。那么你会吗?
注:
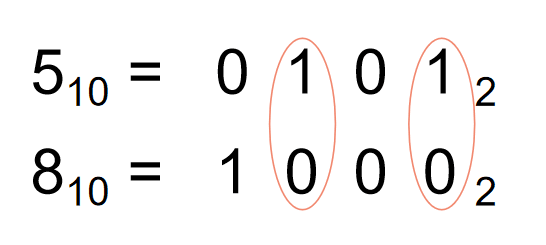
于是,换位大师给小 Y 出了这样一个题:
- 小 Y 要对一个包含 $n$ 个整数的序列进行一些操作。
- 在一次操作中,小 Y 可以选择其中任意两个不同位置上的整数,然后选择它们二进制位上对应的某一位进行交换。
- 小 Y 需要用最少的操作次数,将序列变成一个不递减序列。
但是小 Y 还是不会换位思考,所以他来问你了。那么你会吗?
注:
- “二进制位上对应的位”是指把整数转换为二进制后,从低位往高位数,位置相同的一位。例如:5 转换为二进制后是 0101,8 转换为二进制后是 1000。那么 5 从右往左数的第一个 1,和 8 从右往左数的第一个 0 对应。5 从右往左数的第一个 0,和 8 从右往左数的第二个 0 对应。“不递减序列”指任取 2 ≤ i ≤ n,均满足 a[i-1] ≤ a[i]。
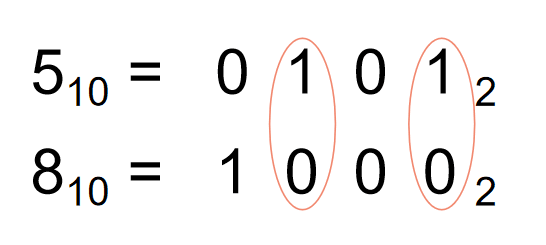
- “不递减序列”指任取 2 ≤ i ≤ n,均满足 a[i-1] ≤ a[i]。
Input
第一行包含一个正整数 $n$,代表序列长度。
第二行包含 $n$ 个整数 a[1], a[2], ..., a[n],代表序列中的每个整数。
第二行包含 $n$ 个整数 a[1], a[2], ..., a[n],代表序列中的每个整数。
Output
一个整数,代表最少所需的操作次数。
Constraints
$1 ≤ n ≤ 100,000$
$0 ≤ a[i] ≤ 3$
$0 ≤ a[i] ≤ 3$
Sample 1 Input
3
1 3 0
Sample 1 Output
1
交换 3 和 0 的高位,序列将变成 1 1 2,满足“不递减序列”的要求。
也就是把 3 和 0 先转为二进制,得到 11 和 00,然后交换左边的那一位,变成 01 和 10,再转回十进制就是 1 和 2 这两个整数。
Sample 2 Input
4
2 1 1 2
Sample 2 Output
2
将第一个数字的高位和第三个数字的高位交换,序列变成 0 1 3 2。
接下来可以把第一个数字的低位和第三个数字的低位交换,序列变成 1 1 2 2。
注意不能直接把第一个数字的高位和第四个数字的低位进行交换!