10968: Codility - NumberOfDiscIntersections
[Creator : ]
Description
Compute the number of intersections in a sequence of discs.
We draw $N$ discs on a plane. The discs are numbered from $0$ to $N − 1$. An array $A$ of $N$ non-negative integers, specifying the radiuses of the discs, is given. The $J$-th disc is drawn with its center at $(J, 0)$ and radius $A[J]$.
We say that the $J$-th disc and $K$-th disc intersect if $J ≠ K$ and the $J$-th and $K$-th discs have at least one common point (assuming that the discs contain their borders).
We draw $N$ discs on a plane. The discs are numbered from $0$ to $N − 1$. An array $A$ of $N$ non-negative integers, specifying the radiuses of the discs, is given. The $J$-th disc is drawn with its center at $(J, 0)$ and radius $A[J]$.
We say that the $J$-th disc and $K$-th disc intersect if $J ≠ K$ and the $J$-th and $K$-th discs have at least one common point (assuming that the discs contain their borders).
Input
Write an efficient algorithm for the following assumptions:
- $N$ is an integer within the range $[0..100,000]$;
- each element of array $A$ is an integer within the range $[0..2,147,483,647]$.
Output
returns the number of (unordered) pairs of intersecting discs.
Sample 1 Input
6
1 5 2 1 4 0
Sample 1 Output
11
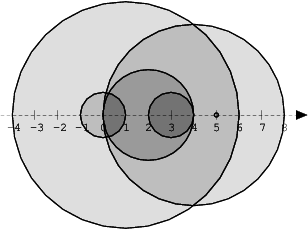
There are eleven (unordered) pairs of discs that intersect, namely:
- discs 1 and 4 intersect, and both intersect with all the other discs;
- disc 2 also intersects with discs 0 and 3.
Sample 2 Input
6
1 1 1 1 1 1
Sample 2 Output
9
Sample 3 Input
3
1 1 1
Sample 3 Output
3