10941: ABC366 - E - Manhattan Multifocal Ellipse
[Creator : ]
Description
You are given $N$ points $(x_1, y_1), (x_2, y_2), \dots, (x_N, y_N)$ on a two-dimensional plane, and a non-negative integer $D$.
Find the number of integer pairs $(x, y)$ such that $\displaystyle \sum_{i=1}^N (|x-x_i|+|y-y_i|) \leq D$.
Find the number of integer pairs $(x, y)$ such that $\displaystyle \sum_{i=1}^N (|x-x_i|+|y-y_i|) \leq D$.
Input
The input is given from Standard Input in the following format:
```
$N$ $D$
$x_1$ $y_1$
$x_2$ $y_2$
$\vdots$
$x_N$ $y_N$
```
```
$N$ $D$
$x_1$ $y_1$
$x_2$ $y_2$
$\vdots$
$x_N$ $y_N$
```
Output
Print the answer.
Constraints
- $1 \leq N \leq 2 \times 10^5$
- $0 \leq D \leq 10^6$
- $-10^6 \leq x_i, y_i \leq 10^6$
- $(x_i, y_i) \neq (x_j, y_j)$ for $i \neq j$.
- All input values are integers.
- $0 \leq D \leq 10^6$
- $-10^6 \leq x_i, y_i \leq 10^6$
- $(x_i, y_i) \neq (x_j, y_j)$ for $i \neq j$.
- All input values are integers.
Sample 1 Input
2 3
0 0
1 0
Sample 1 Output
8
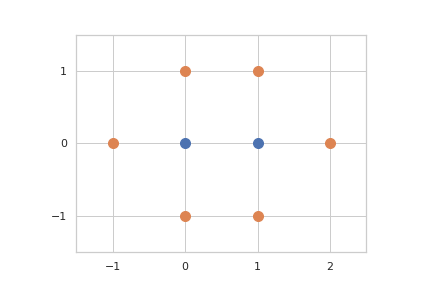
The following figure visualizes the input and the answer for Sample $1$. The blue points represent the input. The blue and red points, eight in total, satisfy the condition in the statement.
Sample 2 Input
2 0
0 0
2 0
Sample 2 Output
0
Sample 3 Input
6 100
9 -6
10 -1
2 10
-1 7
-7 5
-1 -4
Sample 3 Output
419