10936: ABC365 - G - AtCoder Office
[Creator : ]
Description
$N$ people work at the AtCoder office.
The office keeps records of entries and exits, and there have been $M$ entries and exits since the records began.
The $i$-th $(1\leq i\leq M)$ record is represented by a pair of integers $(T_i, P_i)$, indicating that at time $T_i$, the $P_i$-th person either entered the office if they were outside, or exited the office if they were inside.
It is known that all people were outside the office at the beginning of the records, and they are outside now.
Answer $Q$ queries in the following format.
For the $i$-th $(1\leq i\leq Q)$ query, you are given a pair of integers $(A_i, B_i)$. Find the total length of the periods during which both the $A_i$-th and $B_i$-th persons were inside the office since the records began.
The office keeps records of entries and exits, and there have been $M$ entries and exits since the records began.
The $i$-th $(1\leq i\leq M)$ record is represented by a pair of integers $(T_i, P_i)$, indicating that at time $T_i$, the $P_i$-th person either entered the office if they were outside, or exited the office if they were inside.
It is known that all people were outside the office at the beginning of the records, and they are outside now.
Answer $Q$ queries in the following format.
For the $i$-th $(1\leq i\leq Q)$ query, you are given a pair of integers $(A_i, B_i)$. Find the total length of the periods during which both the $A_i$-th and $B_i$-th persons were inside the office since the records began.
Input
The input is given from Standard Input in the following format:
```
$N$ $M$
$T_1$ $P_1$
$T_2$ $P_2$
$\vdots$
$T_M$ $P_M$
$Q$
$A_1$ $B_1$
$A_2$ $B_2$
$\vdots$
$A_Q$ $B_Q$
```
```
$N$ $M$
$T_1$ $P_1$
$T_2$ $P_2$
$\vdots$
$T_M$ $P_M$
$Q$
$A_1$ $B_1$
$A_2$ $B_2$
$\vdots$
$A_Q$ $B_Q$
```
Output
Print $Q$ lines. The $i$-th line $(1\leq i\leq Q)$ should contain the answer to the $i$-th query.
Constraints
- $2\leq N\leq2\times10^5$
- $2\leq M\leq2\times10^5$
- $1\leq T_1\lt T_2\lt\dotsb\lt T_M\leq10^9$
- $1\leq P_i\leq N\ (1\leq i\leq M)$
- For every $1\leq p\leq N$, the number of indices $i$ such that $P_i=p$ is even.
- $1\leq Q\leq2\times10^5$
- $1\leq A_i\lt B_i\leq N\ (1\leq i\leq Q)$
- All inputs are integers.
- $2\leq M\leq2\times10^5$
- $1\leq T_1\lt T_2\lt\dotsb\lt T_M\leq10^9$
- $1\leq P_i\leq N\ (1\leq i\leq M)$
- For every $1\leq p\leq N$, the number of indices $i$ such that $P_i=p$ is even.
- $1\leq Q\leq2\times10^5$
- $1\leq A_i\lt B_i\leq N\ (1\leq i\leq Q)$
- All inputs are integers.
Sample 1 Input
3 8
10 1
20 2
30 1
40 3
60 3
70 1
80 2
90 1
3
1 2
1 3
2 3
Sample 1 Output
20
0
20
The following diagram shows the time each of the three people spent inside the office.
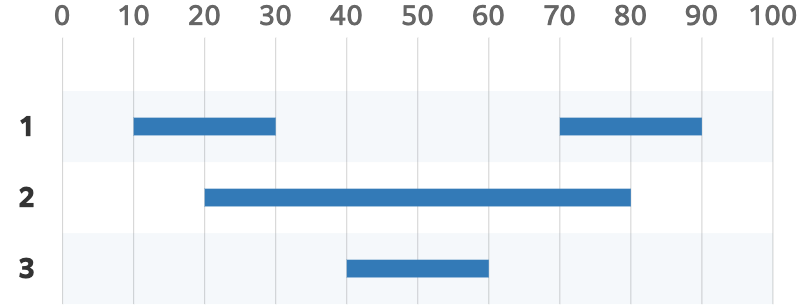
The answers to each query are as follows:

The answers to each query are as follows:
- The 1st and 2nd persons were both inside the office from time $20$ to time $30$ and from time $70$ to time $80$. The lengths of these two periods are both $10$, so print the total, which is $20$.
- The 1st and 3rd persons were never inside the office at the same time, so print $0$.
- The 2nd and 3rd persons were both inside the office from time $40$ to time $60$. The length of this period is $20$, so print $20$.
Sample 2 Input
10 20
10257 9
10490 4
19335 1
25893 5
32538 9
33433 3
38522 9
40629 9
42896 5
52106 1
53024 3
55610 5
56721 9
58286 9
63128 3
70513 3
70977 4
74936 5
79883 9
95116 9
7
1 3
3 9
1 9
4 9
1 5
5 9
3 5
Sample 2 Output
18673
2107
15310
25720
17003
10317
16848