There are infinitely many cells on a plane. For every pair of integers $(x,y)$, there is a corresponding cell, which we will call cell $(x,y)$.

Each cell is either an empty cell or a wall cell.  
You are given two sequences of positive integers of length $N$: $L=(L _ 1,L _ 2,\dotsc,L _ N)$ and $U=(U _ 1,U _ 2,\dotsc,U _ N)$. Here, $L _ i$ and $U _ i$ satisfy $1\leq L _ i\leq U _ i\leq10 ^ 9$ for $i=1,2,\ldots,N$.  
All cells $(x,y)\ (1\leq x\leq N,L _ x\leq y\leq U _ x)$ are empty cells, and all other cells are wall cells.

When Takahashi is at an empty cell $(x,y)$, he can perform one of the following actions.

-   If cell $(x+1,y)$ is an empty cell, move to cell $(x+1,y)$.
-   If cell $(x-1,y)$ is an empty cell, move to cell $(x-1,y)$.
-   If cell $(x,y+1)$ is an empty cell, move to cell $(x,y+1)$.
-   If cell $(x,y-1)$ is an empty cell, move to cell $(x,y-1)$.

It is guaranteed that he can travel between any two empty cells by repeating his actions.

Answer $Q$ queries in the following format.

For the $i$\-th query $(1\leq i\leq Q)$, you are given a quadruple of integers $(s _ {x,i},s _ {y,i},t _ {x,i},t _ {y,i})$. Find the minimum number of actions required for Takahashi to move from cell $(s _ {x,i},s _ {y,i})$ to cell $(t _ {x,i},t _ {y,i})$. For each query, it is guaranteed that the given two cells are empty cells.

The input is given from Standard Input in the following format:

```
$N$
$L _ 1$ $U _ 1$
$L _ 2$ $U _ 2$
$\vdots$
$L _ N$ $U _ N$
$Q$
$s _ {x,1}$ $s _ {y,1}$ $t _ {x,1}$ $t _ {y,1}$
$s _ {x,2}$ $s _ {y,2}$ $t _ {x,2}$ $t _ {y,2}$
$\vdots$
$s _ {x,Q}$ $s _ {y,Q}$ $t _ {x,Q}$ $t _ {y,Q}$
```

Print $Q$ lines. The $i$-th line $(1\leq i\leq Q)$ should contain the answer to the $i$-th query.

-   $1\leq N\leq2\times10 ^ 5$
-   $1\leq L _ i\leq U _ i\leq10 ^ 9\ (1\leq i\leq N)$
-   $\lbrack L _ i,U _ i\rbrack\cap\lbrack L _ {i+1},U _ {i+1}\rbrack\neq\emptyset\ (1\leq i\lt N)$
-   $1\leq Q\leq2\times10 ^ 5$
-   $1\leq s _ {x,i}\leq N$ and $L _ {s _ {x,i}}\leq s _ {y,i}\leq U _ {s _ {x,i}}\ (1\leq i\leq Q)$
-   $1\leq t _ {x,i}\leq N$ and $L _ {t _ {x,i}}\leq t _ {y,i}\leq U _ {t _ {x,i}}\ (1\leq i\leq Q)$
-   All input values are integers.

10
3
14

The given cells are as follows.

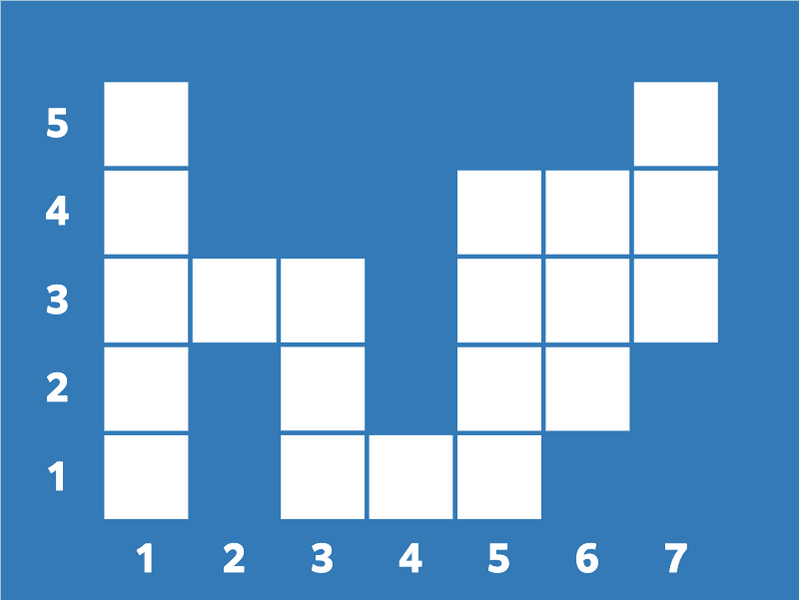
For the first query, for example, Takahashi can move from cell $(1,4)$ to cell $(6,3)$ in ten actions as follows.

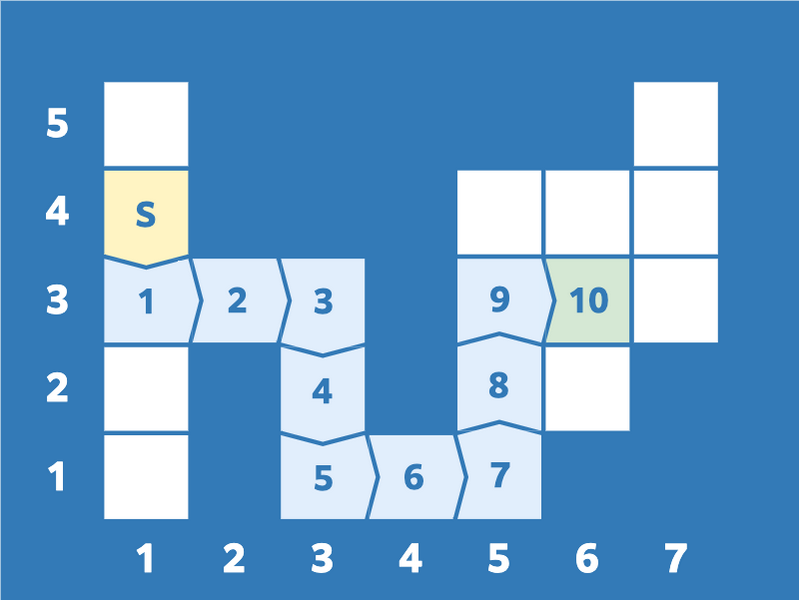
It is impossible to move from cell $(1,4)$ to cell $(6,3)$ in nine or fewer actions, so print $10$.