10910: ABC362 - B - Right Triangle
[Creator : ]
Description
In the $xy$-plane, there are three points $A(x_A, y_A)$, $B(x_B, y_B)$, and $C(x_C, y_C)$ that are not collinear. Determine whether the triangle $ABC$ is a right triangle.
Input
The input is given from Standard Input in the following format:
```
$x_A$ $y_A$
$x_B$ $y_B$
$x_C$ $y_C$
```
```
$x_A$ $y_A$
$x_B$ $y_B$
$x_C$ $y_C$
```
Output
Print Yes if the triangle ABC is a right triangle, and No otherwise.
Constraints
- $-1000 \leq x_A, y_A, x_B, y_B, x_C, y_C \leq 1000$
- The three points $A$, $B$, and $C$ are not collinear.
- All input values are integers.
- The three points $A$, $B$, and $C$ are not collinear.
- All input values are integers.
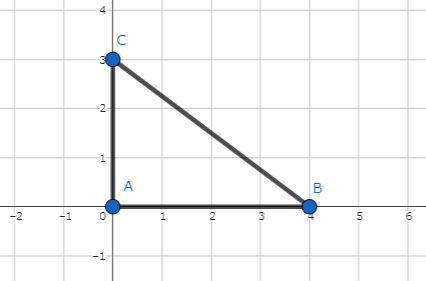
Sample 1 Input
0 0
4 0
0 3
Sample 1 Output
Yes
The triangle $ABC$ is a right triangle.
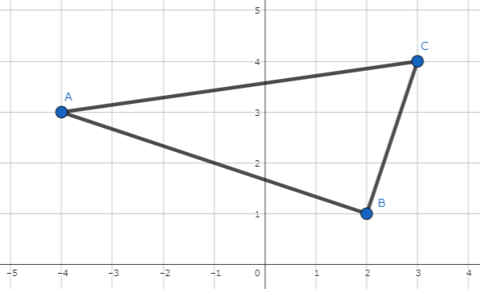
Sample 2 Input
-4 3
2 1
3 4
Sample 2 Output
Yes
The triangle $ABC$ is a right triangle.
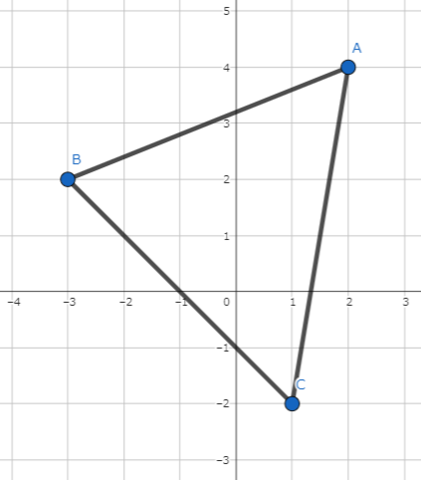
Sample 3 Input
2 4
-3 2
1 -2
Sample 3 Output
No
The triangle $ABC$ is not a right triangle.