10908: ABC361 - G - Go Territory
[Creator : ]
Description
There are $N$ stones placed on a $2$-dimensional plane. The $i$-th stone is located at coordinates $(X_i, Y_i)$. All stones are located at lattice points in the first quadrant (including the axes).
Count the number of lattice points $(x, y)$ where no stone is placed and it is impossible to reach $(-1, -1)$ from $(x, y)$ by repeatedly moving up, down, left, or right by $1$ without passing through coordinates where a stone is placed.
More precisely, count the number of lattice points $(x, y)$ where no stone is placed, and there does not exist a finite sequence of integer pairs $(x_0, y_0), \ldots, (x_k, y_k)$ that satisfies all of the following four conditions:
Count the number of lattice points $(x, y)$ where no stone is placed and it is impossible to reach $(-1, -1)$ from $(x, y)$ by repeatedly moving up, down, left, or right by $1$ without passing through coordinates where a stone is placed.
More precisely, count the number of lattice points $(x, y)$ where no stone is placed, and there does not exist a finite sequence of integer pairs $(x_0, y_0), \ldots, (x_k, y_k)$ that satisfies all of the following four conditions:
- $(x_0, y_0) = (x, y)$.
- $(x_k, y_k) = (-1, -1)$.
- $|x_i - x_{i+1}| + |y_i - y_{i+1}| = 1$ for all $0 \leq i < k$.
- There is no stone at $(x_i, y_i)$ for all $0 \leq i \leq k$.
Input
The input is given from Standard Input in the following format:
```
$N$
$X_1$ $Y_1$
$\vdots$
$X_N$ $Y_N$
```
```
$N$
$X_1$ $Y_1$
$\vdots$
$X_N$ $Y_N$
```
Output
Print the number of lattice points that satisfy the conditions.
Constraints
- $0 \leq N \leq 2 \times 10^5$
- $0 \leq X_i, Y_i \leq 2 \times 10^5$
- The pairs $(X_i, Y_i)$ are distinct.
- All input values are integers.
- $0 \leq X_i, Y_i \leq 2 \times 10^5$
- The pairs $(X_i, Y_i)$ are distinct.
- All input values are integers.
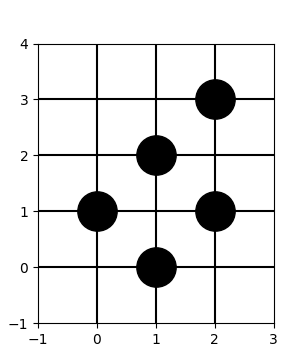
Sample 1 Input
5
1 0
0 1
2 3
1 2
2 1
Sample 1 Output
1
It is impossible to reach $(-1, -1)$ from $(1, 1)$.

Sample 2 Input
0
Sample 2 Output
0
There may be cases where no stones are placed.
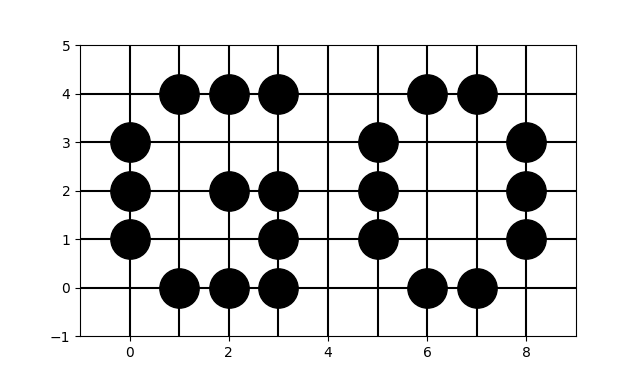
Sample 3 Input
22
0 1
0 2
0 3
1 0
1 4
2 0
2 2
2 4
3 0
3 1
3 2
3 4
5 1
5 2
5 3
6 0
6 4
7 0
7 4
8 1
8 2
8 3
Sample 3 Output
6
There are six such points: $(6, 1), (6, 2), (6, 3), (7, 1), (7, 2), (7, 3)$.