You are trying to implement collision detection in a 3D game.

In a $3$-dimensional space, let $C(a,b,c,d,e,f)$ denote the cuboid with a diagonal connecting $(a,b,c)$ and $(d,e,f)$, and with all faces parallel to the $xy$-plane, $yz$-plane, or $zx$-plane.
(This definition uniquely determines $C(a,b,c,d,e,f)$.)
Given two cuboids $C(a,b,c,d,e,f)$ and $C(g,h,i,j,k,l)$, determine whether their intersection has a positive volume.

The input is given from Standard Input in the following format:

```
$a$ $b$ $c$ $d$ $e$ $f$
$g$ $h$ $i$ $j$ $k$ $l$
```

Print Yes if the intersection of the two cuboids has a positive volume, and No otherwise.

• $0 \leq a < d \leq 1000$
• $0 \leq b < e \leq 1000$
• $0 \leq c < f \leq 1000$
• $0 \leq g < j \leq 1000$
• $0 \leq h < k \leq 1000$
• $0 \leq i < l \leq 1000$
• All input values are integers.

Yes

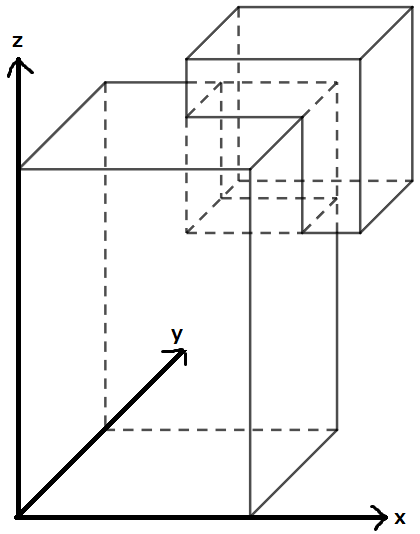
The positional relationship of the two cuboids is shown in the figure below, and their intersection has a volume of $8$.

No

The two cuboids touch at a face, where the volume of the intersection is $0$.