There is a long water tank with boards of different heights placed at equal intervals. Takahashi wants to know the time at which water reaches each section separated by the boards when water is poured from one end of the tank.

You are given a sequence of positive integers of length $N$: $H=(H _ 1,H _ 2,\dotsc,H _ N)$.

There is a sequence of non-negative integers of length $N+1$: $A=(A _ 0,A _ 1,\dotsc,A _ N)$. Initially, $A _ 0=A _ 1=\dotsb=A _ N=0$.

Perform the following operations repeatedly on $A$:

1. Increase the value of $A _ 0$ by $1$.
2. For $i=1,2,\ldots,N$ in this order, perform the following operation:
   • If $A _ {i-1}\gt A _ i$ and $A _ {i-1}\gt H _ i$, decrease the value of $A _ {i-1}$ by 1 and increase the value of $A _ i$ by $1$.

For each $i=1,2,\ldots,N$, find the number of operations before $A _ i>0$ holds for the first time.

The input is given from Standard Input in the following format:

```
$N$
$H _ 1$ $H _ 2$ $\dotsc$ $H _ N$
```

Print the answers for $i=1,2,\ldots,N$ in a single line, separated by spaces.

-   $1\leq N\leq2\times10 ^ 5$
-   $1\leq H _ i\leq10 ^ 9\ (1\leq i\leq N)$
-   All input values are integers.

4 5 13 14 26

The first five operations go as follows.

Here, each row corresponds to one operation, with the leftmost column representing step 1 and the others representing step 2.

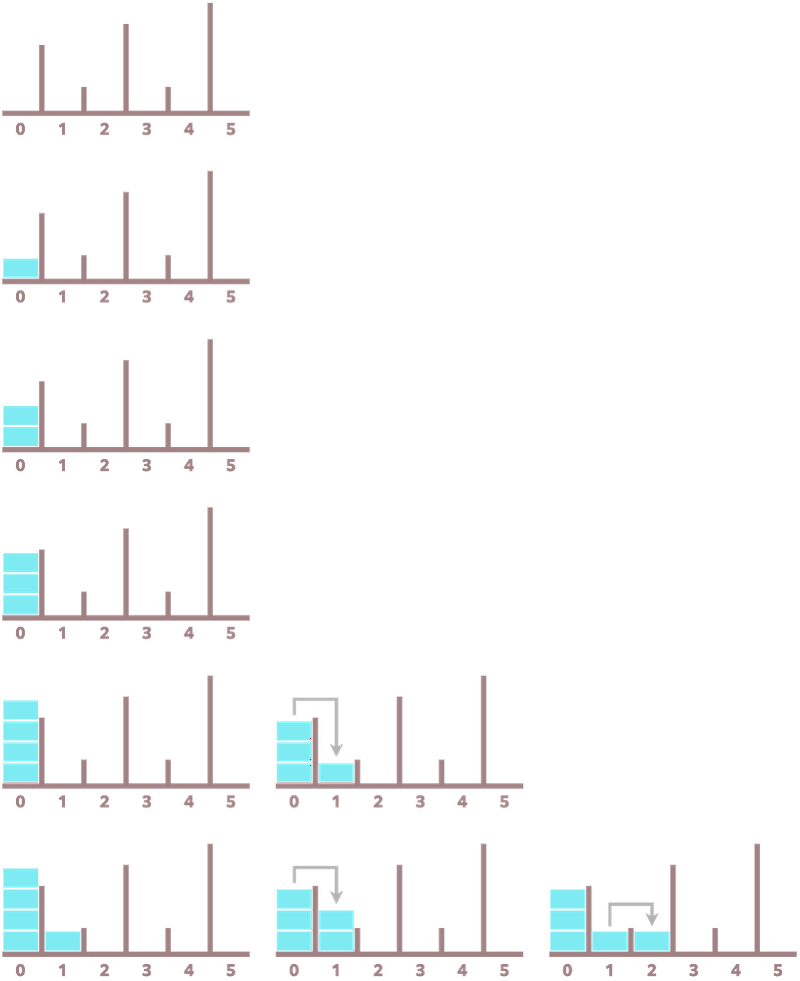
From this diagram, $A _ 1\gt0$ holds for the first time after the 4th operation, and $A _ 2\gt0$ holds for the first time after the 5th operation.

Similarly, the answers for $A _ 3, A _ 4, A _ 5$ are $13, 14, 26$, respectively.

Therefore, you should print 4 5 13 14 26.