The coordinate plane is covered with $2\times1$ tiles. The tiles are laid out according to the following rules:

-   For an integer pair $(i,j)$, the square $A _ {i,j}=\lbrace(x,y)\mid i\leq x\leq i+1\wedge j\leq y\leq j+1\rbrace$ is contained in one tile.
-   When $i+j$ is even, $A _ {i,j}$ and $A _ {i + 1,j}$ are contained in the same tile.

Tiles include their boundaries, and no two different tiles share a positive area.

Near the origin, the tiles are laid out as follows:



Takahashi starts at the point $(S _ x+0.5,S _ y+0.5)$ on the coordinate plane.

He can repeat the following move as many times as he likes:

-   Choose a direction (up, down, left, or right) and a positive integer $n$. Move $n$ units in that direction.

Each time he enters a tile, he pays a toll of $1$.

Find the minimum toll he must pay to reach the point $(T _ x+0.5,T _ y+0.5)$.

The input is given from Standard Input in the following format:

```
$S _ x$ $S _ y$
$T _ x$ $T _ y$
```

Print the minimum toll Takahashi must pay.

-   $0\leq S _ x\leq2\times10 ^ {16}$
-   $0\leq S _ y\leq2\times10 ^ {16}$
-   $0\leq T _ x\leq2\times10 ^ {16}$
-   $0\leq T _ y\leq2\times10 ^ {16}$
-   All input values are integers.

5

For example, Takahashi can pay a toll of $5$ by moving as follows:

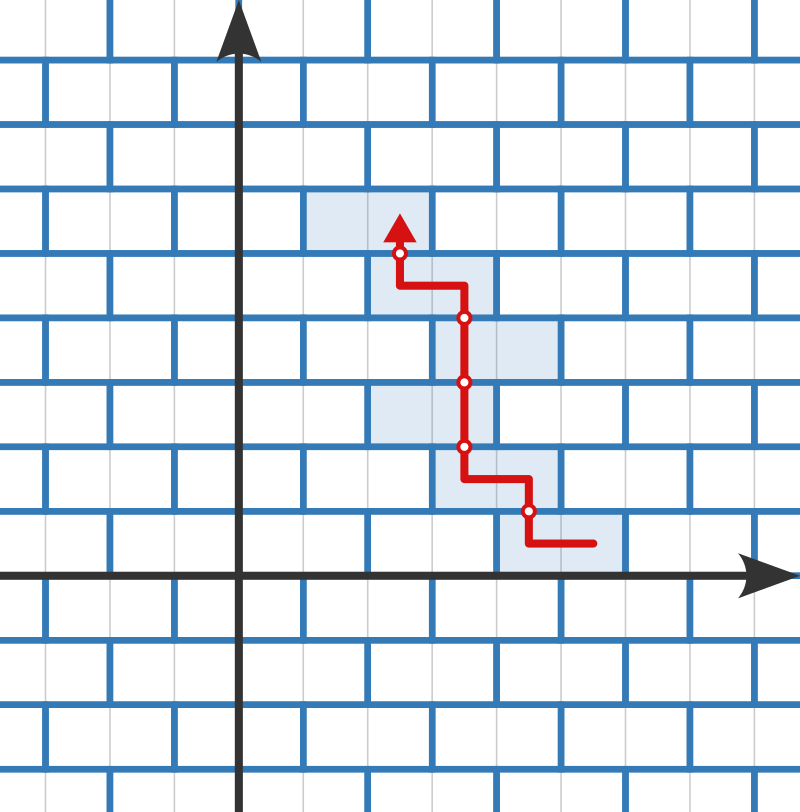
• Move left by $1$. Pay a toll of $0$.
• Move up by $1$. Pay a toll of $1$.
• Move left by $1$. Pay a toll of $0$.
• Move up by $3$. Pay a toll of $3$.
• Move left by $1$. Pay a toll of $0$.
• Move up by $1$. Pay a toll of $1$.

It is impossible to reduce the toll to $4$ or less, so print 5.

0

There are cases where no toll needs to be paid.