10886: ABC358 - F - Easiest Maze
[Creator : ]
Description
Snuke is planning to build a maze as a new attraction in AtCoder Land. The maze is represented as a grid with $N$ rows and $M$ columns, with the top edge of the top-right cell being the entrance and the bottom edge of the bottom-right cell being the exit. He will create the maze by appropriately placing walls between adjacent cells.
He loves simple mazes, so he wants the path from the entrance to the exit to pass through exactly $K$ cells without any branches. Determine if it is possible to create such a maze, and if possible, construct one.
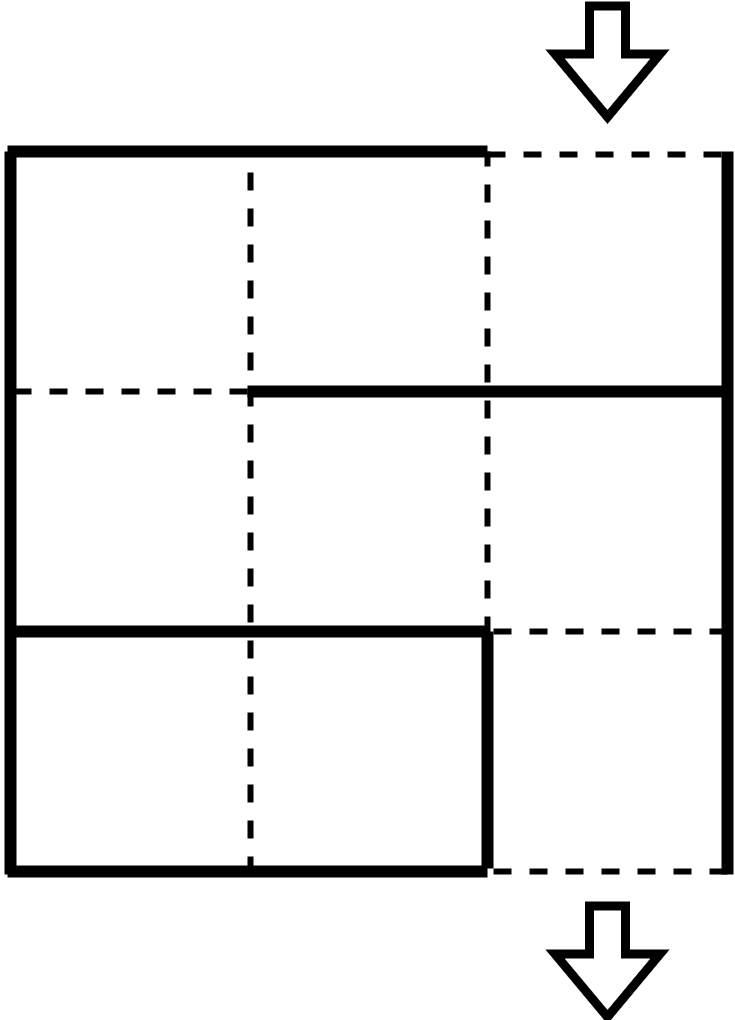
For example, in the following figure, $N=3$ and $M=3$, and walls are placed at the solid lines (walls are always placed around the outer perimeter except for the entrance and exit). In this case, the path from the entrance to the exit passes through exactly $7$ cells without any branches.
Below is a formal statement.
There is a grid with $N$ rows and $M$ columns. Let $(i, j)$ denote the cell at the $i$-th row from the top and $j$-th column from the left. For each pair of side-adjacent cells, you can decide whether to place a wall between them. Determine whether it is possible to place walls to satisfy the following condition, and if it is possible, construct one such placement.
He loves simple mazes, so he wants the path from the entrance to the exit to pass through exactly $K$ cells without any branches. Determine if it is possible to create such a maze, and if possible, construct one.
For example, in the following figure, $N=3$ and $M=3$, and walls are placed at the solid lines (walls are always placed around the outer perimeter except for the entrance and exit). In this case, the path from the entrance to the exit passes through exactly $7$ cells without any branches.

Below is a formal statement.
There is a grid with $N$ rows and $M$ columns. Let $(i, j)$ denote the cell at the $i$-th row from the top and $j$-th column from the left. For each pair of side-adjacent cells, you can decide whether to place a wall between them. Determine whether it is possible to place walls to satisfy the following condition, and if it is possible, construct one such placement.
Consider an undirected graph $G$ with $NM$ vertices. Each vertex of $G$ is uniquely labeled by a pair of integers $(i,j)\ (1\leq i\leq N, 1\leq j\leq M)$. Two distinct vertices $(i_1,j_1)$ and $(i_2,j_2)$ are connected by an edge if and only if $|i_1-i_2|+|j_1-j_2|=1$ and there is no wall between the corresponding cells $(i_1,j_1)$ and $(i_2,j_2)$ on the grid.
Condition: there exists a simple path with $K$ vertices that connects the two vertices $(1,M)$ and $(N,M)$, and the connected component containing the vertices $(1,M)$ and $(N,M)$ consists only of this path.
Input
The input is given from Standard Input in the following format:
$N$ $M$ $K$
$N$ $M$ $K$
Output
If there is no placement of walls that satisfies the condition, print
See also the sample outputs below to better understand the complicated output format.
Yes
+++++ $\dots$ +++S+
+o?o? $\dots$ ?o?o+
+?+?+ $\dots$ +?+?+
+o?o? $\dots$ ?o?o+
+?+?+ $\dots$ +?+?+
$\vdots$
+o?o? $\dots$ ?o?o+
+?+?+ $\dots$ +?+?+
+o?o? $\dots$ ?o?o+
+++++ $\dots$ +++G+
Here,
Below is a formal instruction.
No. Otherwise, print one such placement in the following format. If multiple valid placements exist, any of them can be printed. See also the sample outputs below to better understand the complicated output format.
Yes
+++++ $\dots$ +++S+
+o?o? $\dots$ ?o?o+
+?+?+ $\dots$ +?+?+
+o?o? $\dots$ ?o?o+
+?+?+ $\dots$ +?+?+
$\vdots$
+o?o? $\dots$ ?o?o+
+?+?+ $\dots$ +?+?+
+o?o? $\dots$ ?o?o+
+++++ $\dots$ +++G+
Here,
S, G, +, and o represent the entrance, exit, a wall, and a cell, respectively, and ? between cells represents a position where a wall can be placed. Replace ? between two horizontally adjacent cells with | if a wall is placed, and . otherwise. Replace ? between two vertically adjacent cells with - if a wall is placed, and . otherwise. Below is a formal instruction.
-
The output should consist of $2N+2$ lines. Line $1$ should contain the string
Yes, and lines $2$ to $2N+2$ should contain strings of length $2M+1$ as described below.-
Line $2$ should be a concatenation of
+repeated $2M-1$ times,S, and+, in this order. -
Line $1+2i$ $(1\leq i\leq N)$ should be a concatenation of
+,o, $c_{i,1}$,o, $c_{i,2}$, $\dots$, $c_{i,M-1}$,o,+, in this order. Here, $c_{i,j}$ is|if a wall is placed between cells $(i,j)$ and $(i,j+1)$, and.otherwise. -
Line $2+2i$ $(1\leq i\leq N-1)$ should be a concatenation of
+, $r_{i,1}$,+, $r_{i,2}$,+, $\dots$,+, $r_{i,M}$,+, in this order. Here, $r_{i,j}$ is-if a wall is placed between cells $(i,j)$ and $(i+1,j)$, and.otherwise. -
Line $2N+2$ should be a concatenation of
+repeated $2M-1$ times,G, and+, in this order.
-
Line $2$ should be a concatenation of
Constraints
- $2\leq N \leq 100$
- $1\leq M \leq 100$
- $1\leq K\leq NM$
- All input values are integers.
- $1\leq M \leq 100$
- $1\leq K\leq NM$
- All input values are integers.
Sample 1 Input
3 3 7
Sample 1 Output
Yes
+++++S+
+o.o.o+
+.+-+-+
+o.o.o+
+-+-+.+
+o.o|o+
+++++G+
This is the same placement of walls as in the figure in the problem statement.
Sample 2 Input
3 3 2
Sample 2 Output
No
Sample 3 Input
4 1 4
Sample 3 Output
Yes
+S+
+o+
+.+
+o+
+.+
+o+
+.+
+o+
+G+