We have a grid with $H$ horizontal rows and $W$ vertical columns. Let $(i,j)$ denote the square at the $i$-th row from the top and the $j$-th column from the left.

The square $(i, j)$ has two numbers $A_{ij}$ and $B_{ij}$ written on it.

First, for each square, Takahashi paints one of the written numbers red and the other blue.

Then, he travels from the square $(1, 1)$ to the square $(H, W)$. In one move, he can move from a square $(i, j)$ to the square $(i+1, j)$ or the square $(i, j+1)$. He must not leave the grid.

Let the _unbalancedness_ be the absolute difference of the sum of red numbers and the sum of blue numbers written on the squares along Takahashi's path, including the squares $(1, 1)$ and $(H, W)$.

Takahashi wants to make the unbalancedness as small as possible by appropriately painting the grid and traveling on it.

Find the minimum unbalancedness possible.

Input is given from Standard Input in the following format:

```
$H$ $W$
$A_{11}$ $A_{12}$ $\ldots$ $A_{1W}$
$:$
$A_{H1}$ $A_{H2}$ $\ldots$ $A_{HW}$
$B_{11}$ $B_{12}$ $\ldots$ $B_{1W}$
$:$
$B_{H1}$ $B_{H2}$ $\ldots$ $B_{HW}$
```

Print the minimum unbalancedness possible.

-   $2 \leq H \leq 80$
-   $2 \leq W \leq 80$
-   $0 \leq A_{ij} \leq 80$
-   $0 \leq B_{ij} \leq 80$
-   All values in input are integers.

0

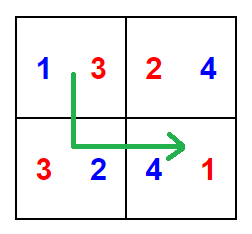
By painting the grid and traveling on it as shown in the figure below, the sum of red numbers and the sum of blue numbers are $3+3+1=7$ and $1+2+4=7$, respectively, for the unbalancedness of $0$.