There is a tree with $N$ vertices numbered $1$ to $N$. The $i$-th edge in this tree connects Vertex $a_i$ and Vertex $b_i$, and the color and length of that edge are $c_i$ and $d_i$, respectively. Here the color of each edge is represented by an integer between $1$ and $N-1$ (inclusive). The same integer corresponds to the same color, and different integers correspond to different colors.

Answer the following $Q$ queries:

-   Query $j$ ($1 \leq j \leq Q$): assuming that the length of every edge whose color is $x_j$ is changed to $y_j$, find the distance between Vertex $u_j$ and Vertex $v_j$. (The changes of the lengths of edges do not affect the subsequent queries.)

Input is given from Standard Input in the following format:

```
$N$ $Q$
$a_1$ $b_1$ $c_1$ $d_1$
$:$
$a_{N-1}$ $b_{N-1}$ $c_{N-1}$ $d_{N-1}$
$x_1$ $y_1$ $u_1$ $v_1$
$:$
$x_Q$ $y_Q$ $u_Q$ $v_Q$
```

Print $Q$ lines. The $j$-th line ($1 \leq j \leq Q$) should contain the answer to Query $j$.

-   $2 \leq N \leq 10^5$
-   $1 \leq Q \leq 10^5$
-   $1 \leq a_i, b_i \leq N$
-   $1 \leq c_i \leq N-1$
-   $1 \leq d_i \leq 10^4$
-   $1 \leq x_j \leq N-1$
-   $1 \leq y_j \leq 10^4$
-   $1 \leq u_j < v_j \leq N$
-   The given graph is a tree.
-   All values in input are integers.

130
200
60

The graph in this input is as follows:

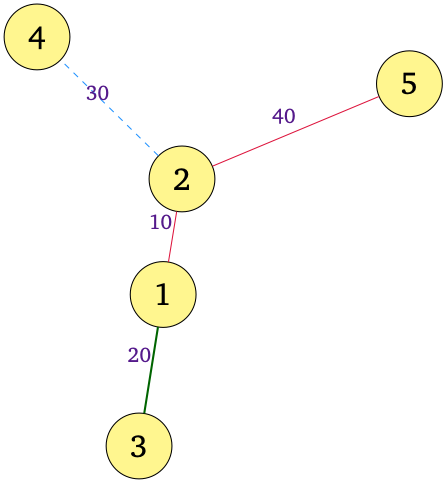
Here the edges of Color $1$ are shown as solid red lines, the edge of Color $2$ is shown as a bold green line, and the edge of Color $4$ is shown as a blue dashed line.

• Query $1$: Assuming that the length of every edge whose color is $1$ is changed to $100$, the distance between Vertex $1$ and Vertex $4$ is $100 + 30 = 130$.
• Query $2$: Assuming that the length of every edge whose color is $1$ is changed to $100$, the distance between Vertex $1$ and Vertex $5$ is $100 + 100 = 200$.
• Query $3$: Assuming that the length of every edge whose color is $3$ is changed to $1000$ (there is no such edge), the distance between Vertex $3$ and Vertex $4$ is $20 + 10 + 30 = 60$. Note that the edges of Color $1$ now have their original lengths.