You are given a tree with $N$ vertices and $N-1$ edges. The vertices are numbered $1$ to $N$, and the $i$-th edge connects Vertex $a_i$ and $b_i$.

You have coloring materials of $K$ colors. For each vertex in the tree, you will choose one of the $K$ colors to paint it, so that the following condition is satisfied:

-   If the distance between two different vertices $x$ and $y$ is less than or equal to two, $x$ and $y$ have different colors.

How many ways are there to paint the tree? Find the count modulo $1\ 000\ 000\ 007$.

What is tree? A tree is a kind of graph. For detail, please see: Wikipedia "Tree (graph theory)"

What is distance? The distance between two vertices $x$ and $y$ is the minimum number of edges one has to traverse to get from $x$ to $y$.

Input is given from Standard Input in the following format:

```
$N$ $K$
$a_1$ $b_1$
$a_2$ $b_2$
$.$
$.$
$.$
$a_{N-1}$ $b_{N-1}$
```

Print the number of ways to paint the tree, modulo $1\ 000\ 000\ 007$.

-   $1 \leq N,K \leq 10^5$
-   $1 \leq a_i,b_i \leq N$
-   The given graph is a tree.

6

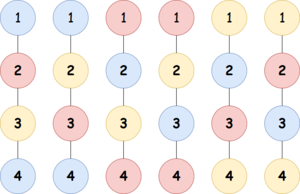
There are six ways to paint the tree.