10633: 初赛集训 课堂测试12-2 数据结构 图论(CSP-S)
[Creator : ]
Description
1. [S-2015-20](多选)以下图中一定可以进行黑白染色的有()。(黑白染色:为各个结点分别指定黑白两种颜色之一,使相邻结点颜色不同。)
A. 二分图
B. 完全图
C. 树
D. 连通图
2. [S-2015-14]对图 G 中各个结点分别指定一种颜色,使相邻结点颜色不同,则称为图 G 的一个正常着色。正常着色图 G 所必需的最少颜色数,称为 G 的色数。那么下图的色数是( )。
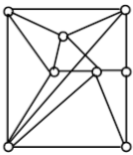
A. 3
B. 4
C. 5
D. 6
3. [S-2021-15]有如下的有向图,节点为 A,B,⋯,J, 其中每条边的长度都标在图中。则节点 A 到节点 J 的最短路径长度为()。
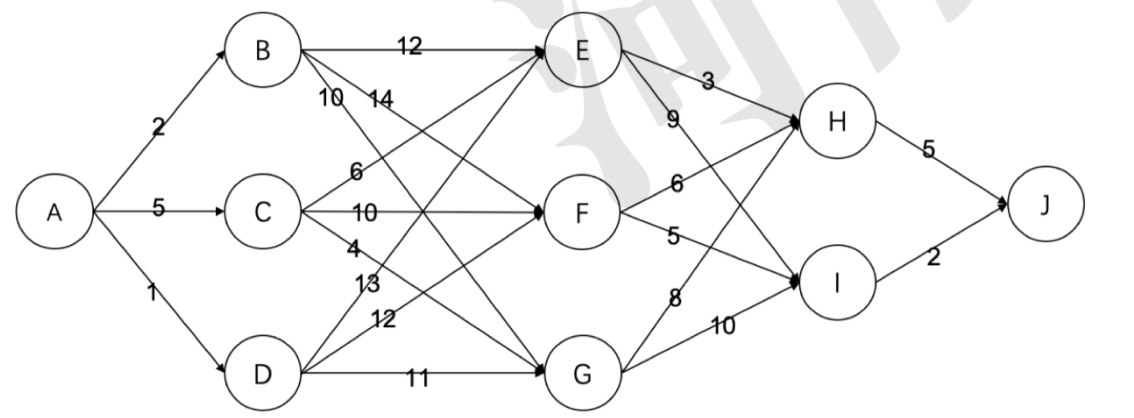
A. 16
B. 19
C. 20
D. 22
4. [S-2018-13](多选)下列关于最短路算法的说法正确的有( )。
A. 当图中不存在负权回路但是存在负权边时,Dijkstra 算法不一定能求出源点到所有点的最短路。
B. 当图中不存在负权边时,调用多次 Dijkstra 算法能求出每对顶点间最短路径。
C. 图中存在负权回路时,调用一次 Dijkstra 算法也一定能求出源点到所有点的最短路。
D. 当图中不存在负权边时,调用一次 Dijkstra 算法不能用于每对顶点间最短路计算。
5. [S-2023-13]如图是一张包含 6 个顶点的有向图,但顶点间不存在拓扑序。如果要删除其中一条边,使这 6 个顶点能进行拓扑排序,请问总共有多少条边可以作为候选的被删除边?()
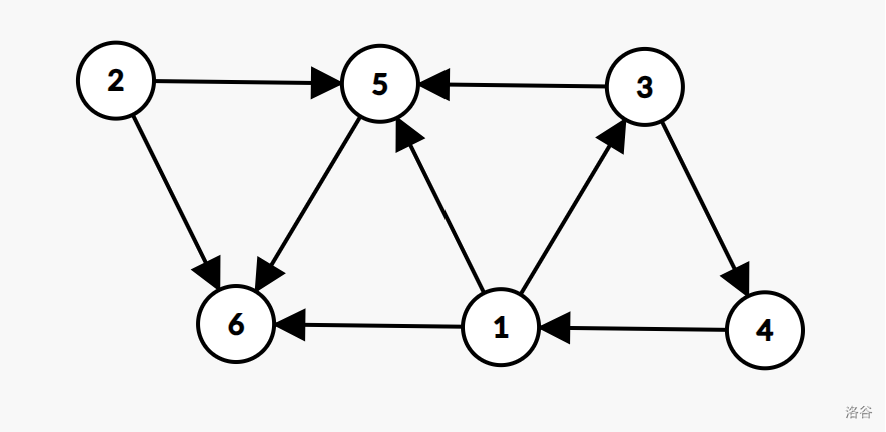
A. 1
B. 2
C. 3
D. 4
6. [S-2015-9][J-2015-12]6 个顶点的连通图的最小生成树,其边数为( )。
A. 6
B. 5
C. 7
D. 4
7. [J-2013-10]在一个无向图中,如果任意两点之间都存在路径相连,则称其为连通图。下图是一个有4 个顶点、 6 条边的连通图。若要使它不再是连通图,至少要删去其中的( )条边。
A. 1
B. 2
C. 3
D. 4
8. [J-2009-18]已知n个顶点的有向图,若该图是强连通的(从所有顶点都存在路径到达其他顶点),则该图中最少有多少条有向边
A. n
B. n+1
C. n-1
D. n(n-1)
9. [S-2012-16](多选)已知带权有向图 G 上的所有权值均为正整数,记顶点 u 到顶点 v 的最短路径的权值为 d(u,v)。若 v1, v2, v3, v4, v5 是图 G 上的顶点,且它们之间两两都存在路径可达,则以下说法正确的有( )。
A. v1到 v2的最短路径可能包含一个环
B. d(v1,v2)=d(v2,v1)
C. d(v1,v3)≤ d(v1,v2)+d(v2,v3)
D. 如果 v1→ v2→ v3→ v4→ v5 是 v1到 v5的一条最短路径,那么 v2→v3→v4是 v2 到 v4的一条最短路径
10. [S-2009-9]从V0开始用 prim 算法求最小生成树。则依次加入最小生成树的顶点集合的顶点序列为:
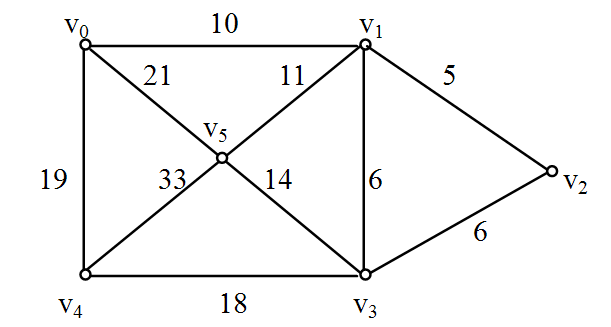
A. V0, V1, V2, V3, V5, V4
B. V0, V1, V5, V4, V3, V3
C. V1, V2, V3, V0, V5, V4
D. V1, V2, V3, V0, V4, V5
A. 二分图
B. 完全图
C. 树
D. 连通图
2. [S-2015-14]对图 G 中各个结点分别指定一种颜色,使相邻结点颜色不同,则称为图 G 的一个正常着色。正常着色图 G 所必需的最少颜色数,称为 G 的色数。那么下图的色数是( )。

A. 3
B. 4
C. 5
D. 6
3. [S-2021-15]有如下的有向图,节点为 A,B,⋯,J, 其中每条边的长度都标在图中。则节点 A 到节点 J 的最短路径长度为()。

A. 16
B. 19
C. 20
D. 22
4. [S-2018-13](多选)下列关于最短路算法的说法正确的有( )。
A. 当图中不存在负权回路但是存在负权边时,Dijkstra 算法不一定能求出源点到所有点的最短路。
B. 当图中不存在负权边时,调用多次 Dijkstra 算法能求出每对顶点间最短路径。
C. 图中存在负权回路时,调用一次 Dijkstra 算法也一定能求出源点到所有点的最短路。
D. 当图中不存在负权边时,调用一次 Dijkstra 算法不能用于每对顶点间最短路计算。
5. [S-2023-13]如图是一张包含 6 个顶点的有向图,但顶点间不存在拓扑序。如果要删除其中一条边,使这 6 个顶点能进行拓扑排序,请问总共有多少条边可以作为候选的被删除边?()

A. 1
B. 2
C. 3
D. 4
6. [S-2015-9][J-2015-12]6 个顶点的连通图的最小生成树,其边数为( )。
A. 6
B. 5
C. 7
D. 4
7. [J-2013-10]在一个无向图中,如果任意两点之间都存在路径相连,则称其为连通图。下图是一个有4 个顶点、 6 条边的连通图。若要使它不再是连通图,至少要删去其中的( )条边。
A. 1
B. 2
C. 3
D. 4
8. [J-2009-18]已知n个顶点的有向图,若该图是强连通的(从所有顶点都存在路径到达其他顶点),则该图中最少有多少条有向边
A. n
B. n+1
C. n-1
D. n(n-1)
9. [S-2012-16](多选)已知带权有向图 G 上的所有权值均为正整数,记顶点 u 到顶点 v 的最短路径的权值为 d(u,v)。若 v1, v2, v3, v4, v5 是图 G 上的顶点,且它们之间两两都存在路径可达,则以下说法正确的有( )。
A. v1到 v2的最短路径可能包含一个环
B. d(v1,v2)=d(v2,v1)
C. d(v1,v3)≤ d(v1,v2)+d(v2,v3)
D. 如果 v1→ v2→ v3→ v4→ v5 是 v1到 v5的一条最短路径,那么 v2→v3→v4是 v2 到 v4的一条最短路径
10. [S-2009-9]从V0开始用 prim 算法求最小生成树。则依次加入最小生成树的顶点集合的顶点序列为:

A. V0, V1, V2, V3, V5, V4
B. V0, V1, V5, V4, V3, V3
C. V1, V2, V3, V0, V5, V4
D. V1, V2, V3, V0, V4, V5