10597: ABC357 —— G - Stair-like Grid
[Creator : ]
Description
There is a special grid with $N$ rows. ($N$ is even.) The $i$-th row from the top has $\left \lceil \frac{i}{2} \right \rceil \times 2$ cells from the left end.
For example, when $N = 6$, the grid looks like the following:
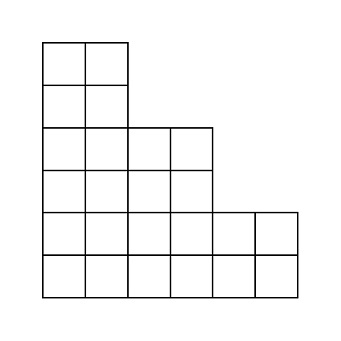
Let $(i, j)$ denote the cell at the $i$\-th row from the top and $j$-th column from the left.
Each cell is either an empty cell or a wall cell. There are $M$ wall cells, and the $i$-th wall cell is $(a_i, b_i)$. Here, $(1, 1)$ and $(N, N)$ are empty.
Starting from $(1, 1)$, how many ways are there to reach $(N, N)$ by repeatedly moving right or down to an adjacent empty cell? Find the count modulo $998244353$.
For example, when $N = 6$, the grid looks like the following:

Let $(i, j)$ denote the cell at the $i$\-th row from the top and $j$-th column from the left.
Each cell is either an empty cell or a wall cell. There are $M$ wall cells, and the $i$-th wall cell is $(a_i, b_i)$. Here, $(1, 1)$ and $(N, N)$ are empty.
Starting from $(1, 1)$, how many ways are there to reach $(N, N)$ by repeatedly moving right or down to an adjacent empty cell? Find the count modulo $998244353$.
Input
The input is given from Standard Input in the following format:
```
$N$ $M$
$a_1$ $b_1$
$a_2$ $b_2$
$\vdots$
$a_M$ $b_M$
```
```
$N$ $M$
$a_1$ $b_1$
$a_2$ $b_2$
$\vdots$
$a_M$ $b_M$
```
Output
Print the number of ways to reach $(N, N)$ from $(1, 1)$ by repeatedly moving right or down to an adjacent empty cell, modulo $998244353$.
Constraints
- $2 \leq N \leq 2.5 \times 10^5$
- $N$ is even.
- $0 \leq M \leq 50$
- $1 \leq a_i \leq N$
- $1 \leq b_i \leq \left \lceil \frac{a_i}{2} \right \rceil \times 2$
- $(a_i, b_i) \neq (1, 1)$ and $(a_i, b_i) \neq (N, N)$.
- $(a_i, b_i) \neq (a_j, b_j)$ if $i \neq j$.
- All input values are integers.
- $N$ is even.
- $0 \leq M \leq 50$
- $1 \leq a_i \leq N$
- $1 \leq b_i \leq \left \lceil \frac{a_i}{2} \right \rceil \times 2$
- $(a_i, b_i) \neq (1, 1)$ and $(a_i, b_i) \neq (N, N)$.
- $(a_i, b_i) \neq (a_j, b_j)$ if $i \neq j$.
- All input values are integers.
Sample 1 Input
4 2
2 1
4 2
Sample 1 Output
2
There are two paths that satisfy the conditions of the problem:
- $(1, 1) \to (1, 2) \to (2, 2) \to (3, 2) \to (3, 3) \to (3, 4) \to (4, 4)$
- $(1, 1) \to (1, 2) \to (2, 2) \to (3, 2) \to (3, 3) \to (4, 3) \to (4, 4)$
Sample 2 Input
6 3
2 1
3 3
4 2
Sample 2 Output
0
Sample 3 Input
100 10
36 9
38 5
38 30
45 1
48 40
71 52
85 27
86 52
92 34
98 37
Sample 3 Output
619611437
100000 10
552 24
4817 255
7800 954
23347 9307
28028 17652
39207 11859
48670 22013
74678 53158
75345 45891
88455 4693
175892766