10573: ABC123 —— C - Five Transportations
Description
There are five means of transport in this empire:
- Train: travels from City $1$ to $2$ in one minute. A train can occupy at most $A$ people.
- Bus: travels from City $2$ to $3$ in one minute. A bus can occupy at most $B$ people.
- Taxi: travels from City $3$ to $4$ in one minute. A taxi can occupy at most $C$ people.
- Airplane: travels from City $4$ to $5$ in one minute. An airplane can occupy at most $D$ people.
- Ship: travels from City $5$ to $6$ in one minute. A ship can occupy at most $E$ people.
For each of them, one vehicle leaves the city at each integer time (time $0$, $1$, $2$, $...$).
There is a group of $N$ people at City $1$, and they all want to go to City $6$.
At least how long does it take for all of them to reach there? You can ignore the time needed to transfer.
Input
```
$N$
$A$
$B$
$C$
$D$
$E$
```
Output
Constraints
- All values in input are integers.
Sample 1 Input
5
3
2
4
3
5
Sample 1 Output
7
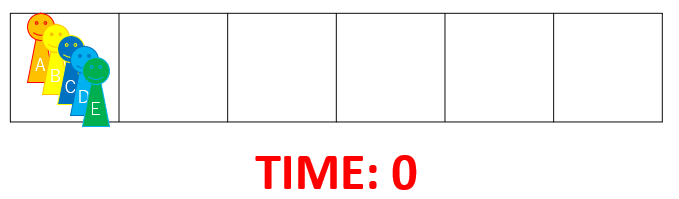
One possible way to travel is as follows. First, there are N=5 people at City 1, as shown in the following image:
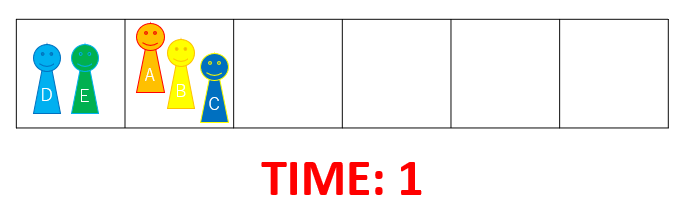
In the first minute, three people travels from City 1 to City 2 by train. Note that a train can only occupy at most three people.
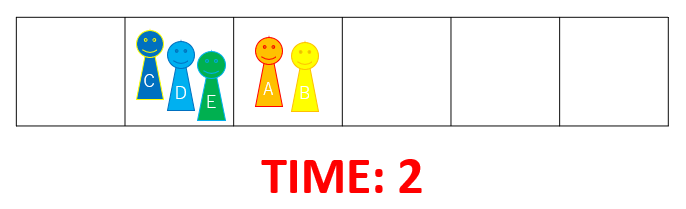
In the second minute, the remaining two people travels from City 1 to City 2 by train, and two of the three people who were already at City 2 travels to City 3 by bus. Note that a bus can only occupy at most two people.
In the third minute, two people travels from City 2 to City 3 by train, and another two people travels from City 3 to City 4 by taxi.

From then on, if they continue traveling without stopping until they reach City 6, all of them can reach there in seven minutes.
There is no way for them to reach City 6 in 6 minutes or less.
Sample 2 Input
10
123
123
123
123
123
Sample 2 Output
5
Sample 3 Input
10000000007
2
3
5
7
11
Sample 3 Output
5000000008