10522: ABC113 —— D - Number of Amidakuji
[Creator : ]
Description
Amidakuji is a traditional method of lottery in Japan.
To make an amidakuji, we first draw $W$ parallel vertical lines, and then draw horizontal lines that connect them. The length of each vertical line is $H+1$ [cm], and the endpoints of the horizontal lines must be at $1, 2, 3, ...,$ or $H$ [cm] from the top of a vertical line.
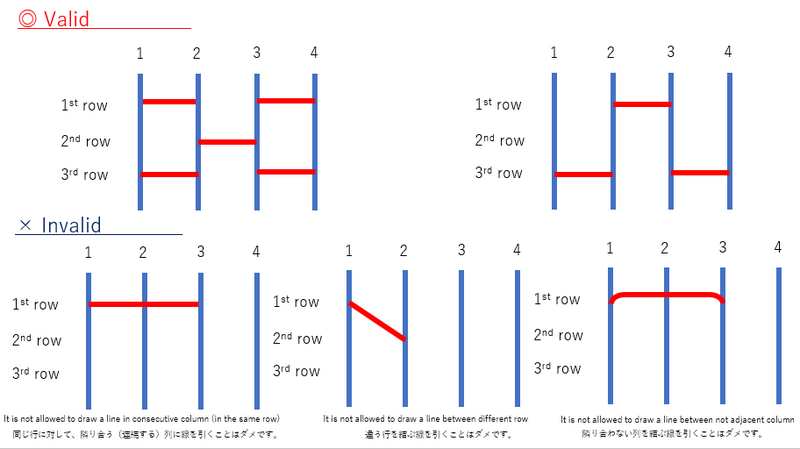
A valid amidakuji is an amidakuji that satisfies the following conditions:
- No two horizontal lines share an endpoint.
- The two endpoints of each horizontal lines must be at the same height.
- A horizontal line must connect adjacent vertical lines.
Find the number of the valid amidakuji that satisfy the following condition, modulo $1\ 000\ 000\ 007$: if we trace the path from the top of the leftmost vertical line to the bottom, always following horizontal lines when we encounter them, we reach the bottom of the $K$\-th vertical line from the left.
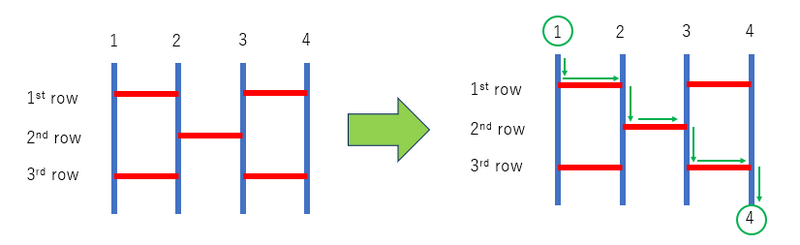
For example, in the following amidakuji, we will reach the bottom of the fourth vertical line from the left.
To make an amidakuji, we first draw $W$ parallel vertical lines, and then draw horizontal lines that connect them. The length of each vertical line is $H+1$ [cm], and the endpoints of the horizontal lines must be at $1, 2, 3, ...,$ or $H$ [cm] from the top of a vertical line.
A valid amidakuji is an amidakuji that satisfies the following conditions:
- No two horizontal lines share an endpoint.
- The two endpoints of each horizontal lines must be at the same height.
- A horizontal line must connect adjacent vertical lines.

Find the number of the valid amidakuji that satisfy the following condition, modulo $1\ 000\ 000\ 007$: if we trace the path from the top of the leftmost vertical line to the bottom, always following horizontal lines when we encounter them, we reach the bottom of the $K$\-th vertical line from the left.
For example, in the following amidakuji, we will reach the bottom of the fourth vertical line from the left.

Input
Input is given from Standard Input in the following format:
```
$H$ $W$ $K$
```
```
$H$ $W$ $K$
```
Output
Print the number of the amidakuji that satisfy the condition, modulo $1\ 000\ 000\ 007$.
Constraints
- $H$ is an integer between $1$ and $100$ (inclusive).
- $W$ is an integer between $1$ and $8$ (inclusive).
- $K$ is an integer between $1$ and $W$ (inclusive).
- $W$ is an integer between $1$ and $8$ (inclusive).
- $K$ is an integer between $1$ and $W$ (inclusive).
Sample 1 Input
1 3 2
Sample 1 Output
1
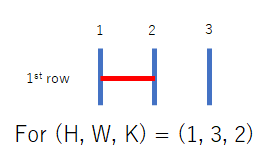
Only the following one amidakuji satisfies the condition:

Sample 2 Input
1 3 1
Sample 2 Output
2
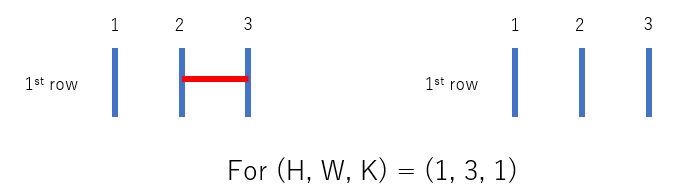
Only the following two amidakuji satisfy the condition:

Sample 3 Input
2 3 3
Sample 3 Output
1
Only the following one amidakuji satisfies the condition:
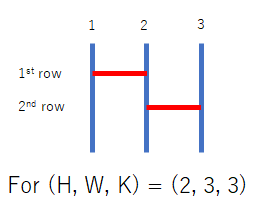

2 3 1
5
Only the following five amidakuji satisfy the condition:
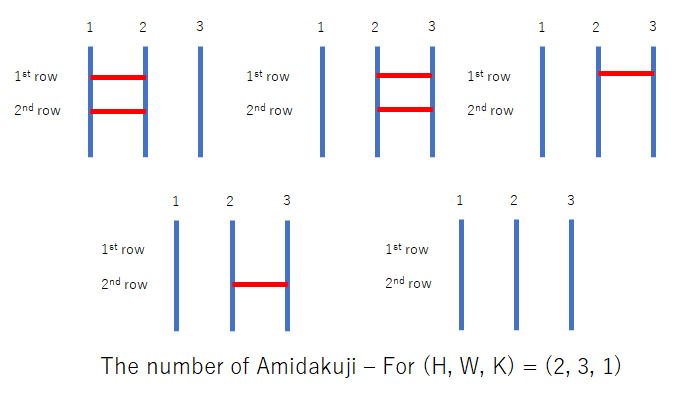

Sample 4 Input
15 8 5
Sample 4 Output
437760187