给你一棵树（即一个连通、无向、无环图），根节点是节点 $1$，这棵树由编号从 $0$ 到 $n$ 的 $n$ 个节点组成。用下标从 $1$ 开始、长度为 $n$ 的数组 $parent$ 来表示这棵树，其中 parent[i] 是节点 $i$ 的父节点，由于节点 $0$ 是根节点，所以 parent[1] == -1 。
另给你一个字符串 $s$，长度也是 $n$，其中 s[i] 表示分配给节点 i 的字符。
请你找出路径上任意一对相邻节点都没有分配到相同字符的最长路径，并返回该路径的长度。

第一样包括一个个整数，第一个整数是 $n\ (1\leq n \leq 5\times 10^5)$，表示节点的数量。
第二行包括 $n$ 个整数，第 $i$ 个整数表示 $parent[i]\ (1 \leq parent[i] \leq n)$。
第三行一个字符串 $s$，s 仅由小写英文字母组成。
保证数据输入合法。

一行一个整数，表示答案。

3

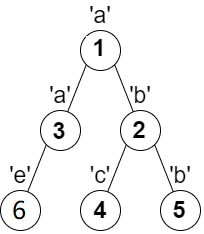
任意一对相邻节点字符都不同的最长路径是：1 -> 2 -> 4。该路径的长度是 3，所以返回 3。 可以证明不存在满足上述条件且比 3 更长的路径。

3

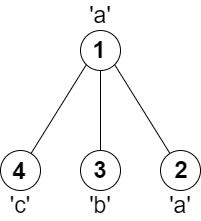
任意一对相邻节点字符都不同的最长路径是：3 -> 1 -> 4。该路径的长度为 3，所以返回 3。