You are given a binary tree with $N$ vertices. The vertices are numbered $1$ to $N$, with vertex $1$ being the root. The $i$\-th edge $(1\leq i \leq N-1)$ connects vertex $i+1$ and vertex $P_i\ (\leq i)$ bidirectionally.

There are one basket and $M$ balls on this tree. The balls are numbered $1$ to $M$, and each ball $j$ has a designated start vertex $S_j$ and goal vertex $T_j$. Initially, the basket is empty and placed at vertex $1$, and the balls are placed at their respective start vertices.

You can perform the following operation any number of times in any order.

-   Let $v$ be the current vertex where the basket is placed. Do one of the following:
    -   Choose one edge connected to vertex $v$, and move the basket along that edge to the adjacent vertex. The balls inside the basket move together with it.
    -   Choose a ball with the start vertex $v$ that is still placed at $v$, and put it into the basket. This operation can only be performed if the basket contains fewer than $K$ balls (that is, the basket cannot contain $K+1$ or more balls).
    -   Choose a ball with the goal vertex $v$ from the basket and take it out, placing it at vertex $v$.

A sequence of operations is called a good operation sequence if and only if the basket is eventually empty and placed at vertex $1$, and the balls are eventually placed at their respective goal vertices.

Since it is tiring to move the basket many times, the basket's movement path should traverse each edge exactly twice before returning to vertex $1$. Find the number, modulo $998244353$, of those paths such that a good operation sequence exists following that path.

The input is given from Standard Input in the following format:

```
$N$ $M$ $K$
$P_1$ $P_2$ $\dots$ $P_{N-1}$
$S_1$ $T_1$
$S_2$ $T_2$
$\vdots$
$S_M$ $T_M$
```

Print the number, modulo $998244353$, of paths traversing every edge exactly twice before returning to vertex $1$ such that a good operation sequence exists following that path.

-   $2\leq N \leq 10^4$
-   $1\leq M \leq 2\times 10^5$
-   $1\leq K \leq 10^3$
-   $1\leq P_i \leq i$
-   For every $v\ (1\leq v \leq N)$, there are at most two $i$'s such that $P_i=v$.
-   $1\leq S_j, T_j \leq N$
-   $S_j \neq T_j$
-   All input values are integers.

1

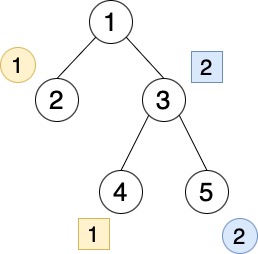
The given graph is shown in the figure below. The circles and squares written next to the vertices represent the start and goal vertices of the balls, respectively.

Among the paths where every edge is traversed exactly twice before returning to vertex 11, there is only one path such that a good operation sequence exists following that path, which is shown below:



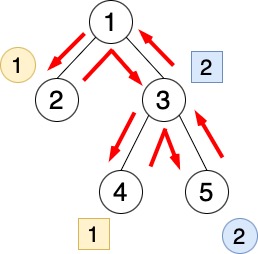
Here, you can construct the following good operation sequence:

1. Move the basket to vertex 2.
2. Put ball 1 into the basket.
3. Move the basket to vertex 1.
4. Move the basket to vertex 3.
5. Move the basket to vertex 4.
6. Take ball 1 out of the basket and place it at vertex 4.
7. Move the basket to vertex 3.
8. Move the basket to vertex 5.
9. Put ball 2 into the basket.
10. Move the basket to vertex 3.
11. Take ball 2 out of the basket and place it at vertex 3.
12. Move the basket to vertex 1.

2

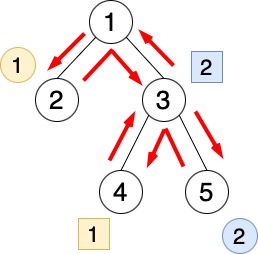
The value of K has increased by 1 from Sample Input 1. This allows you to construct a good operation sequence for the following path, in addition to the one illustrated above.