10379: ABC328 —— E - Modulo MST
[Creator : ]
Description
You are given a weighted simple connected undirected graph with $N$ vertices and $M$ edges, where vertices are numbered $1$ to $N$, and edges are numbered $1$ to $M$. Additionally, a positive integer $K$ is given.
Edge $i\ (1\leq i\leq M)$ connects vertices $u_i$ and $v_i$ and has a weight of $w_i$.
For a spanning tree $T$ of this graph, the cost of $T$ is defined as the sum, modulo $K$, of the weights of the edges in $T$. Find the minimum cost of a spanning tree of this graph.
Edge $i\ (1\leq i\leq M)$ connects vertices $u_i$ and $v_i$ and has a weight of $w_i$.
For a spanning tree $T$ of this graph, the cost of $T$ is defined as the sum, modulo $K$, of the weights of the edges in $T$. Find the minimum cost of a spanning tree of this graph.
Input
The input is given from Standard Input in the following format:
```
$N$ $M$ $K$
$u_1$ $v_1$ $w_1$
$u_2$ $v_2$ $w_2$
$\vdots$
$u_M$ $v_M$ $w_M$
```
```
$N$ $M$ $K$
$u_1$ $v_1$ $w_1$
$u_2$ $v_2$ $w_2$
$\vdots$
$u_M$ $v_M$ $w_M$
```
Output
Print the answer.
Constraints
- $2\leq N\leq8$
- $N-1\leq M\leq\dfrac{N(N-1)}2$
- $1\leq K\leq10^{15}$
- $1\leq u_i\lt v_i\leq N\ (1\leq i\leq M)$
- $0\leq w_i\lt K\ (1\leq i\leq M)$
- The given graph is simple and connected.
- All input values are integers.
- $N-1\leq M\leq\dfrac{N(N-1)}2$
- $1\leq K\leq10^{15}$
- $1\leq u_i\lt v_i\leq N\ (1\leq i\leq M)$
- $0\leq w_i\lt K\ (1\leq i\leq M)$
- The given graph is simple and connected.
- All input values are integers.
Sample 1 Input
5 6 328
1 2 99
1 3 102
2 3 86
2 4 94
2 5 95
3 4 81
Sample 1 Output
33
The given graph is shown below:
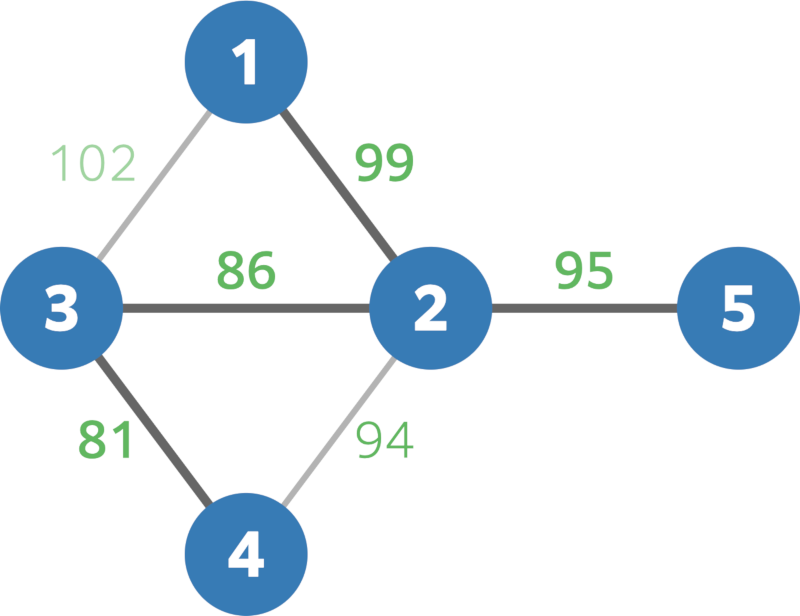
The cost of the spanning tree containing edges 1,3,5,6 is (99+86+81+95) mod 328=361 mod 328=33. The cost of every spanning tree of this graph is at least 33, so print 33.
Sample 2 Input
6 5 998244353
1 2 337361568
1 6 450343304
2 3 61477244
2 5 745383438
4 5 727360840
Sample 2 Output
325437688
Sample 3 Input
8 28 936294041850197
1 2 473294720906780
1 3 743030800139244
1 4 709363019414774
1 5 383643612490312
1 6 557102781022861
1 7 623179288538138
1 8 739618599410809
2 3 857687812294404
2 4 893923168139714
2 5 581822471860662
2 6 740549363586558
2 7 307226438833222
2 8 447399029952998
3 4 636318083622768
3 5 44548707643622
3 6 307262781240755
3 7 12070267388230
3 8 700247263184082
4 5 560567890325333
4 6 704726113717147
4 7 588263818615687
4 8 549007536393172
5 6 779230871080408
5 7 825982583786498
5 8 713928998174272
6 7 751331074538826
6 8 449873635430228
7 8 11298381761479
Sample 3 Output
11360716373