You are given a weighted undirected connected graph $G$ with $N$ vertices and $N-1$ edges, where vertices are numbered $1$ to $N$ and edges are numbered $1$ to $N-1$. Edge $i$ connects vertices $a_i$ and $b_i$ with a weight of $c_i$.

You are given $Q$ queries to process sequentially. The $i$-th query is described as follows:

-   You are given integers $u_i, v_i, w_i$. Add an edge with weight $w_i$ between vertices $u_i$ and $v_i$ in $G$. Then, print the sum of the weights of the edges in a minimum spanning tree of $G$.

The input is given from Standard Input in the following format:

```
$N$ $Q$
$a_1$ $b_1$ $c_1$
$\vdots$
$a_{N-1}$ $b_{N-1}$ $c_{N-1}$
$u_1$ $v_1$ $w_1$
$\vdots$
$u_Q$ $v_Q$ $w_Q$
```

Print $Q$ lines. The $i$-th line should contain the answer to the $i$-th query.

-   $2 \leq N \leq 2 \times 10^5$
-   $1 \leq Q \leq 2 \times 10^5$
-   $1 \leq a_i < b_i \leq N$
-   $1 \leq u_i < v_i \leq N$
-   $1 \leq c_i, w_i \leq 10$
-   The graph is connected before processing the queries.
-   All input values are integers.

12
10
10
7

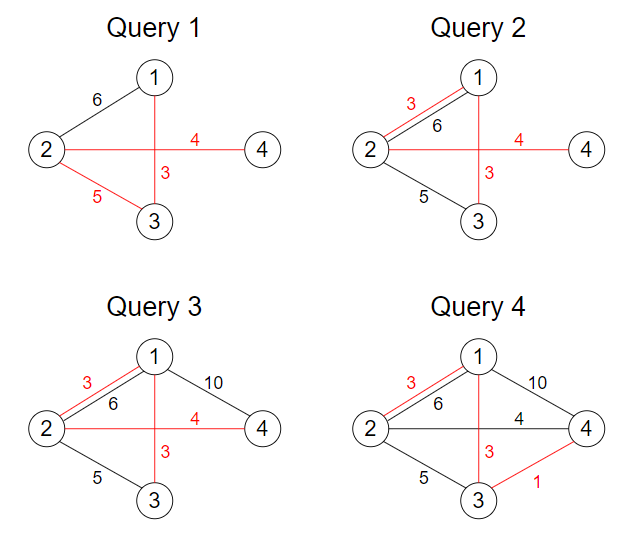
Here is the graph after adding the edge for each query. The edges included in the minimum spanning tree are colored red.