The pattern of AtCoder's wallpaper can be represented on the $xy$-plane as follows:

-   The plane is divided by the following three types of lines:
    -   $x = n$ (where $n$ is an integer)
    -   $y = n$ (where $n$ is an even number)
    -   $x + y = n$ (where $n$ is an even number)
-   Each region is painted black or white. Any two regions adjacent along one of these lines are painted in different colors.
-   The region containing $(0.5, 0.5)$ is painted black.

The following figure shows a part of the pattern.


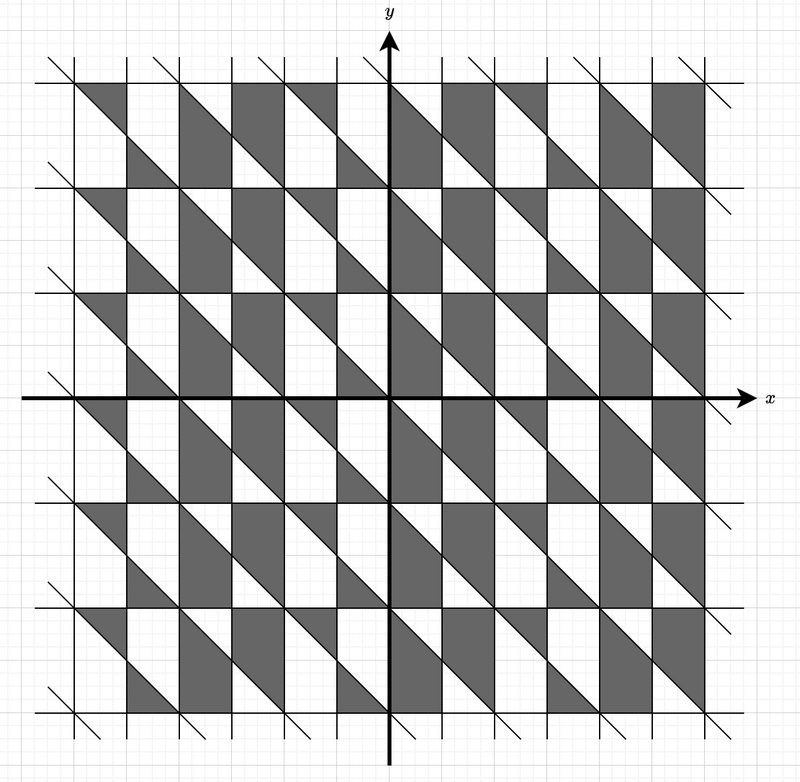
You are given integers $A, B, C, D$. Consider a rectangle whose sides are parallel to the $x$\- and $y$\-axes, with its bottom-left vertex at $(A, B)$ and its top-right vertex at $(C, D)$. Calculate the area of the regions painted black inside this rectangle, and print twice that area.

It can be proved that the output value will be an integer.

The input is given from Standard Input in the following format:

```
$A$ $B$ $C$ $D$
```

Print the answer on a single line.

-   $-10^9 \leq A, B, C, D \leq 10^9$
-   $A < C$ and $B < D$.
-   All input values are integers.

10

We are to find the area of the black-painted region inside the following square:

The area is 5, so print twice that value: 10.

11

The area is 5.5, which is not an integer, but the output value is an integer.