10185: 学习系列 —— 字符串 —— AC自动机
[Creator : ]
Description
AC 自动机是 以 Trie 的结构为基础,结合 KMP 的思想 建立的自动机,用于解决多模式匹配等任务。
简单来说,建立一个 AC 自动机有两个步骤:
Trie 中的结点表示的是某个模式串的前缀。我们在后文也将其称作状态。一个结点表示一个状态,Trie 的边就是状态的转移。
形式化地说,对于若干个模式串 $s_1,s_2,\cdots,s_n$,将它们构建一棵字典树后的所有状态的集合记作
$s_1,s_2,\cdots,s_n$,将它们构建一棵字典树后的所有状态的集合记作  $Q$。
$Q$。
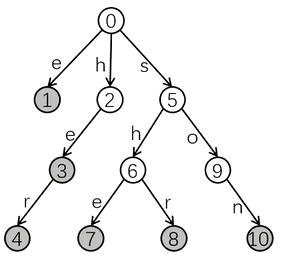
对字符串 e he her she shr son 组成的字典树如图所示。
简单来说,建立一个 AC 自动机有两个步骤:
- 基础的 Trie 结构:将所有的模式串构成一棵 Trie。
- KMP 的思想:对 Trie 树上所有的结点构造失配指针。
【数据结构定义】
建议使用结构体来定义所有数据,这样我们可以根据题目要求,任意增加数据。//AC自动机数据结构
//在Trie中增加了 fail 指针
struct TRIENODE{
int son[28];//叶子
int fail;//AC自动机fail
int end;//以自己为终点字符串出现的次数
//缺省构造函数
TRIENODE(){
fail=end=0;
for(int i=0;i<26;i++){
son[i]=0;
}
}
};
std::vector<TRIENODE> tree;
【数据初始化】
有些题目有 $T$ 组测试用例,这样题目,每次我们都需要对数据初始化。//初始化
void init(){
//清空数据
tree.clear();
//插入第一个节点
tree.push_back(TRIENODE());
}
【字典树构建】
AC 自动机在初始时会将若干个模式串丢到一个 Trie 里,然后在 Trie 上建立 AC 自动机。这个 Trie 就是普通的 Trie,该怎么建怎么建。Trie 中的结点表示的是某个模式串的前缀。我们在后文也将其称作状态。一个结点表示一个状态,Trie 的边就是状态的转移。
形式化地说,对于若干个模式串
对字符串 e he her she shr son 组成的字典树如图所示。

//Trie树中插入字符串s
//和标准Trie一样
int insert(const std::string &s){
int p = 0;//插入位置
for (const auto &ch : s){
int c = ch - 'a';
if(tree[p].son[c]==0){
//儿子不存在,增加新节点
tree.push_back(TRIENODE());
tree[p].son[c]=tree.size()-1;
}
p = tree[p].son[c];
}
tree[p].end++;
return p;
}
Input
【构建AC自动机】
AC 自动机利用一个 fail 指针来辅助多模式串的匹配。状态 $u$ 的 fail 指针指向另一个状态 $v$
- 共同点:两者同样是在失配的时候用于跳转的指针。
- 不同点:next 指针求的是最长 Border(即最长的相同前后缀),而 fail 指针指向所有模式串的前缀中匹配当前状态的最长后缀。
没看懂上面的对比不要急,你只需要知道,AC 自动机的失配指针指向当前状态的最长后缀状态即可。
AC 自动机在做匹配时,同一位上可匹配多个模式串。
3. 构建指针 下面介绍构建 fail 指针的 基础思想:(强调!基础思想!基础!)
构建 fail 指针,可以参考 KMP 中构造 Next 指针的思想。
考虑字典树中当前的结点
-
如果 trie[fail[p],c] 存在:则让 u 的 fail 指针指向 。相当于在 $p$
和 fail[p]
后面加一个字符 c,分别对应 u
和 fail$\left[u \right]$。
-
如果trie[fail[p],c] 不存在:那么我们继续找到 trie[fail[fail[p]],c]
。重复 1 的判断过程,一直跳 fail 指针直到根结点。
- 如果真的没有,就让 fail 指针指向根结点。
【代码解析】
$nxt\left[v\right]$ 保存节点 v 的回跳边的终点。$nxt\left[7\right]=3$回跳边指向父节点的回跳边所指节点的儿子。四个点($v, u, nxt\left[u\right], trie\left[ \right] \left[ \right]$)构成四边形。回跳边所指节点一定是当前节点的最长后缀。
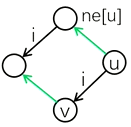
$trie\left[u\right]\left[i\right]$ 存节点 u 的树边的终点。$trie\left[6\right]\left[e\right]=7$。
$trie\left[u\right]\left[i\right]$ 存节点 u 的转移边的终点。$trie\left[7\right]\left[r\right]=4$,转移边指向当前节点的回跳边所指节点的儿子。
三个点($u, nxt\left[u\right], trie\left[\right]\left[\right]$)构成三角形。

转移边所指节点一定是当前节点的最短路。
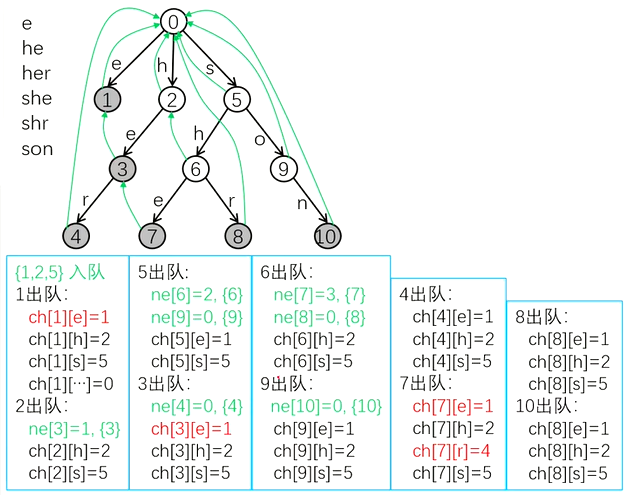
我们使用 BFS 构造 AC自动机。
1. 初始化,吧根节点的儿子们入队。
2. 只要队不空,节点 u 出队。枚举 u 的 26 个儿子。
2.1 如果儿子存在,则跌帮儿子建回跳边,并吧儿子入队。
2.2 如果儿子不存在,则爹自建转移边。
//使用BFS构建AC自动机,构造回跳边和转移边
//即生成nxt的值
void build(){
std::queue<int> que;
//BFS初始状态
for(int i=0;i<26;i++){
if(tree[0].son[i]>0){
que.emplace(tree[0].son[i]);
}
}
while(que.size()){
int p=que.front();
que.pop();
for(int i=0;i<26;i++){
int v=tree[p].son[i];
if(v==0){
//儿子不存在
//爹自建转移边
tree[p].son[i]=tree[tree[p].fail].son[i];
}else{
//儿子存在
//爹帮儿子建回跳边
tree[v].fail=tree[tree[p].fail].son[i];
//儿子入队
que.emplace(v);
}
}
}
}
Output
【简单匹配查询】
在一个主串中,查询匹配字符串出现的次数。我们只需要在 Trie 树中查询即可。
//查询主串
int query(const std::string &s){
int p=0, res=0;
for(const char ch:s){
p=tree[p].son[ch-'a'];//转移
for(int j=p; j && tree[j].end>0; j=tree[j].fail){
res+=tree[j].end;
tree[j].end=0;
}
}
return res;
}
Constraints
【AC自动机和KMP比对】
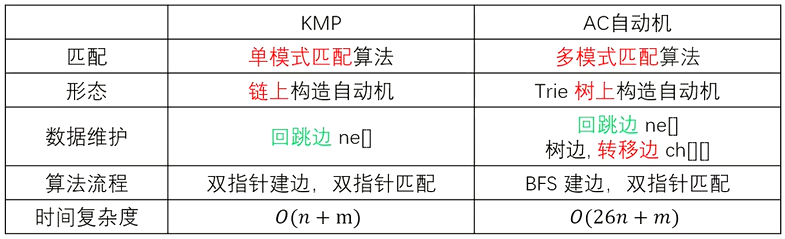
其中,$n$ 是模式串长度,$m$ 是主串长度。
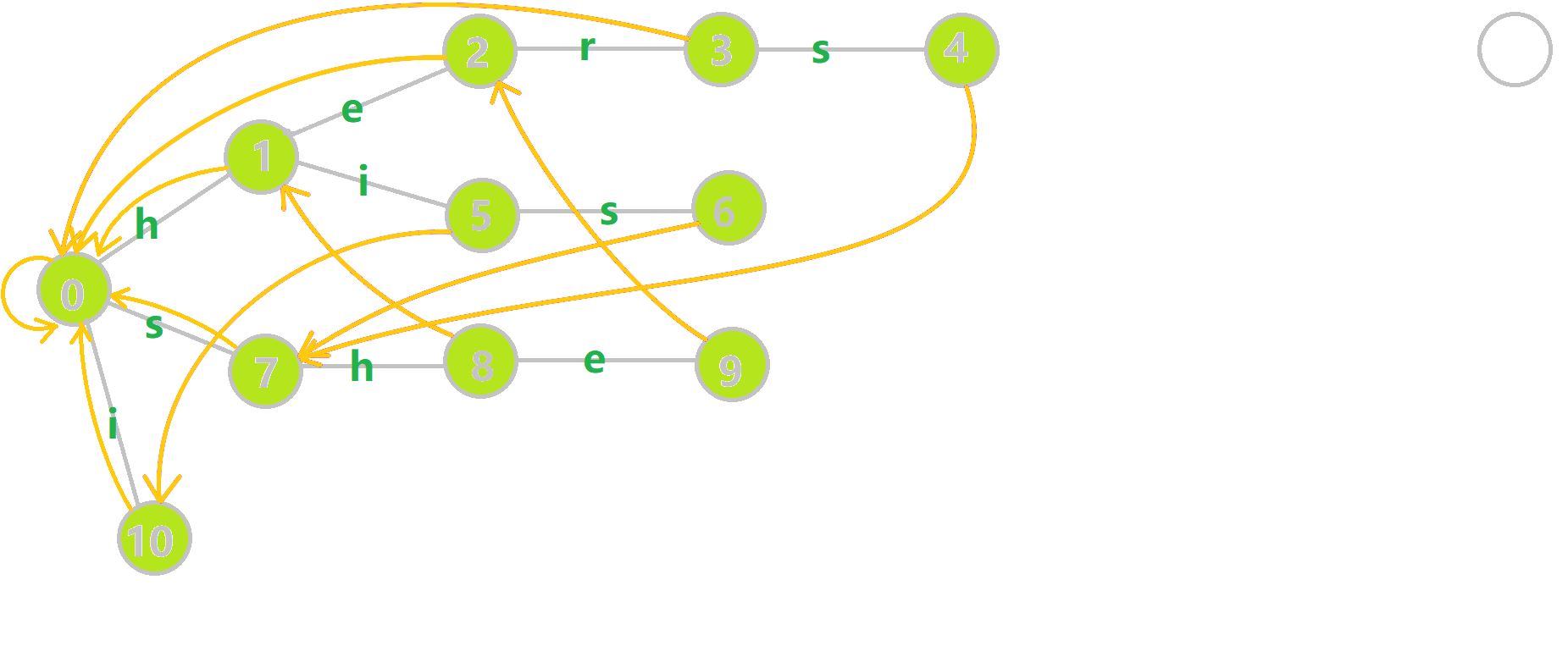
对字符串 hers his she i he 组成的字典树构建 fail 指针:
-
黄色结点:当前的结点
u。
- 绿色结点:表示已经 BFS 遍历完毕的结点,
- 橙色的边:fail 指针。
- 红色的边:当前求出的 fail 指针。
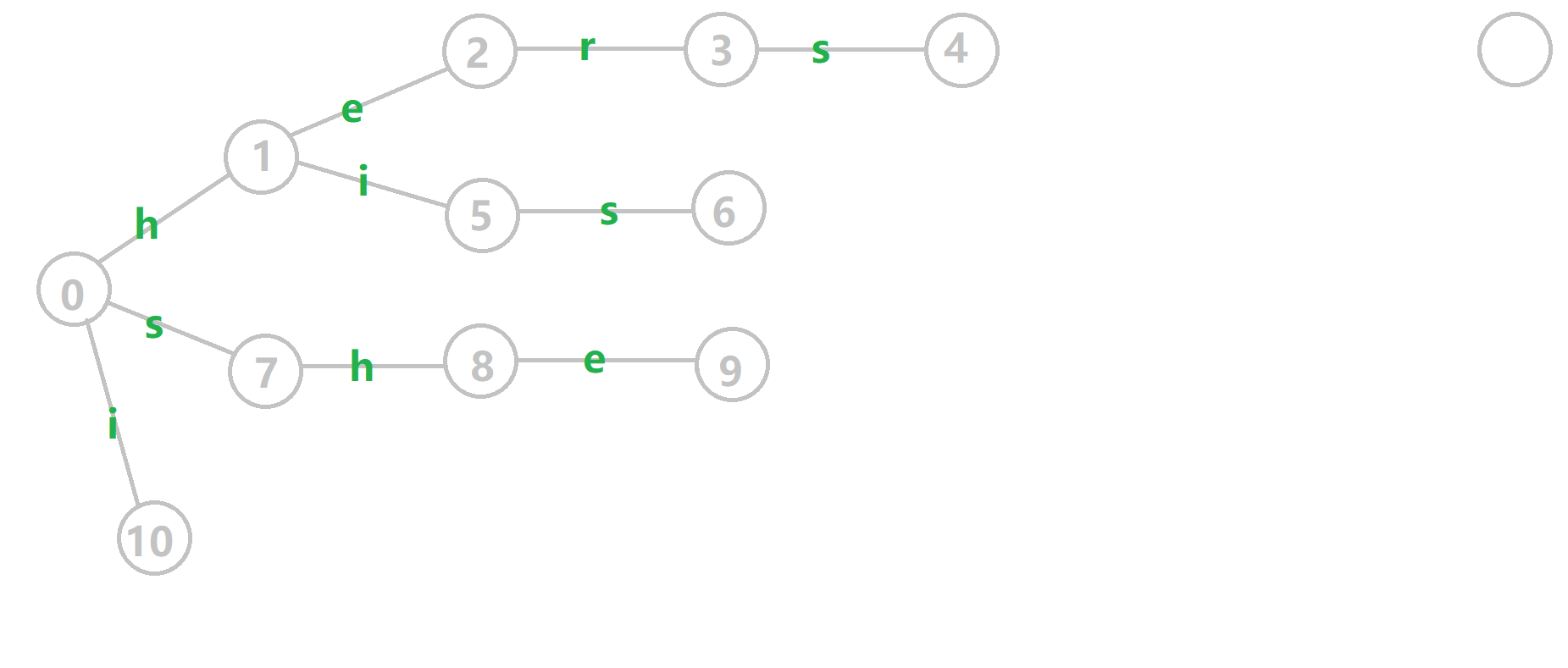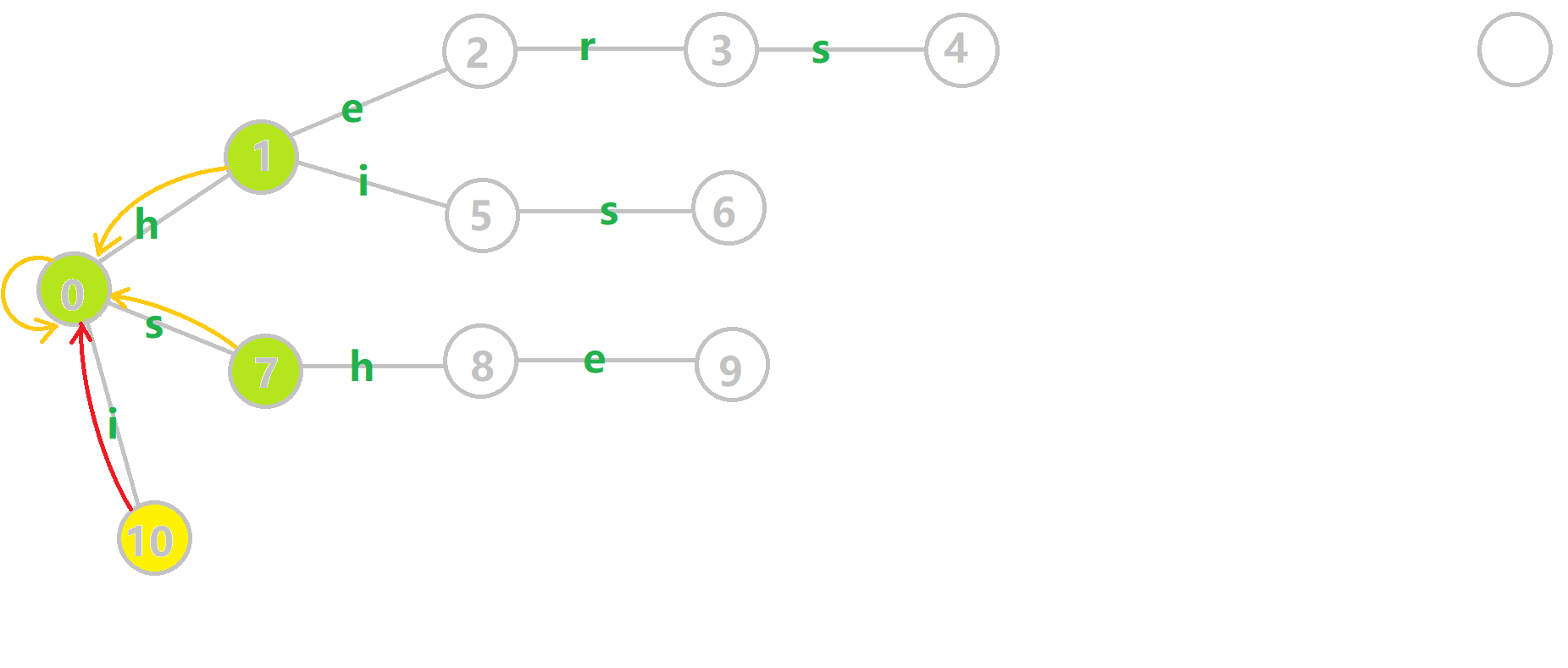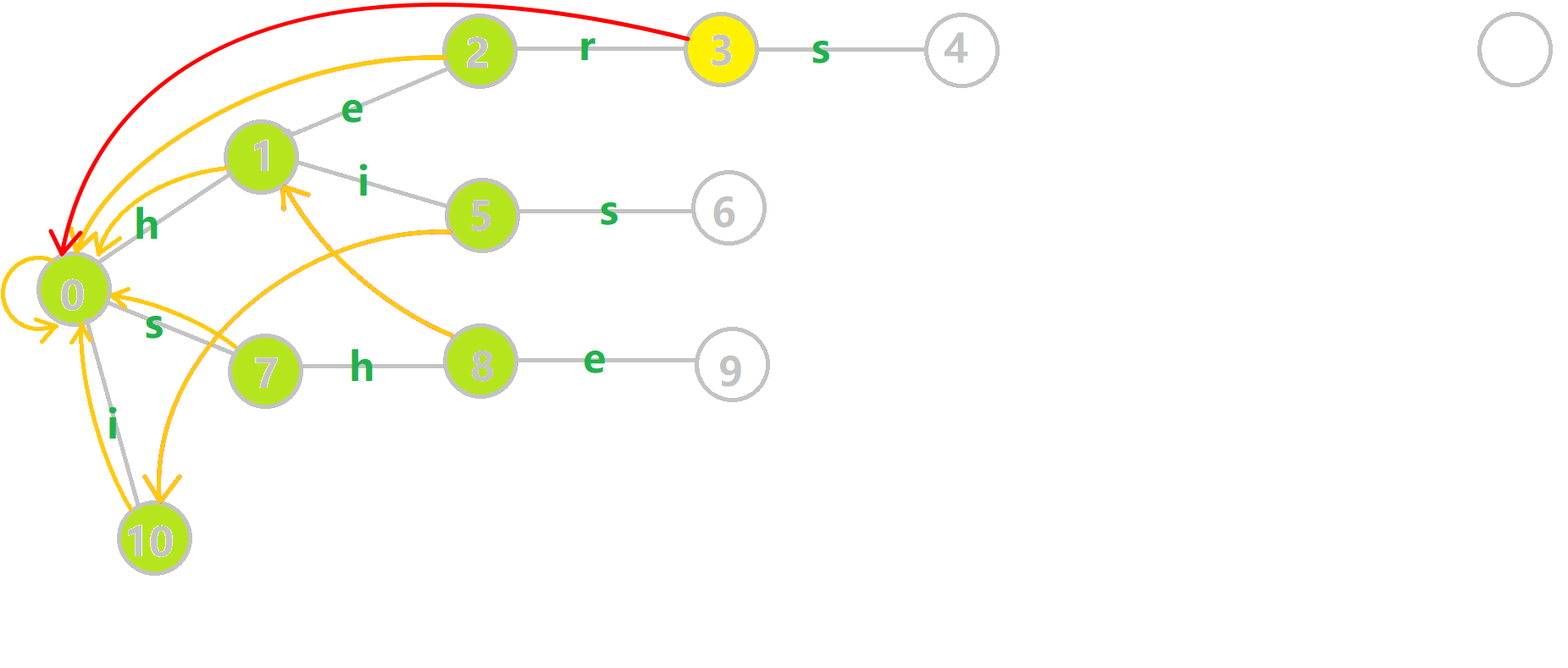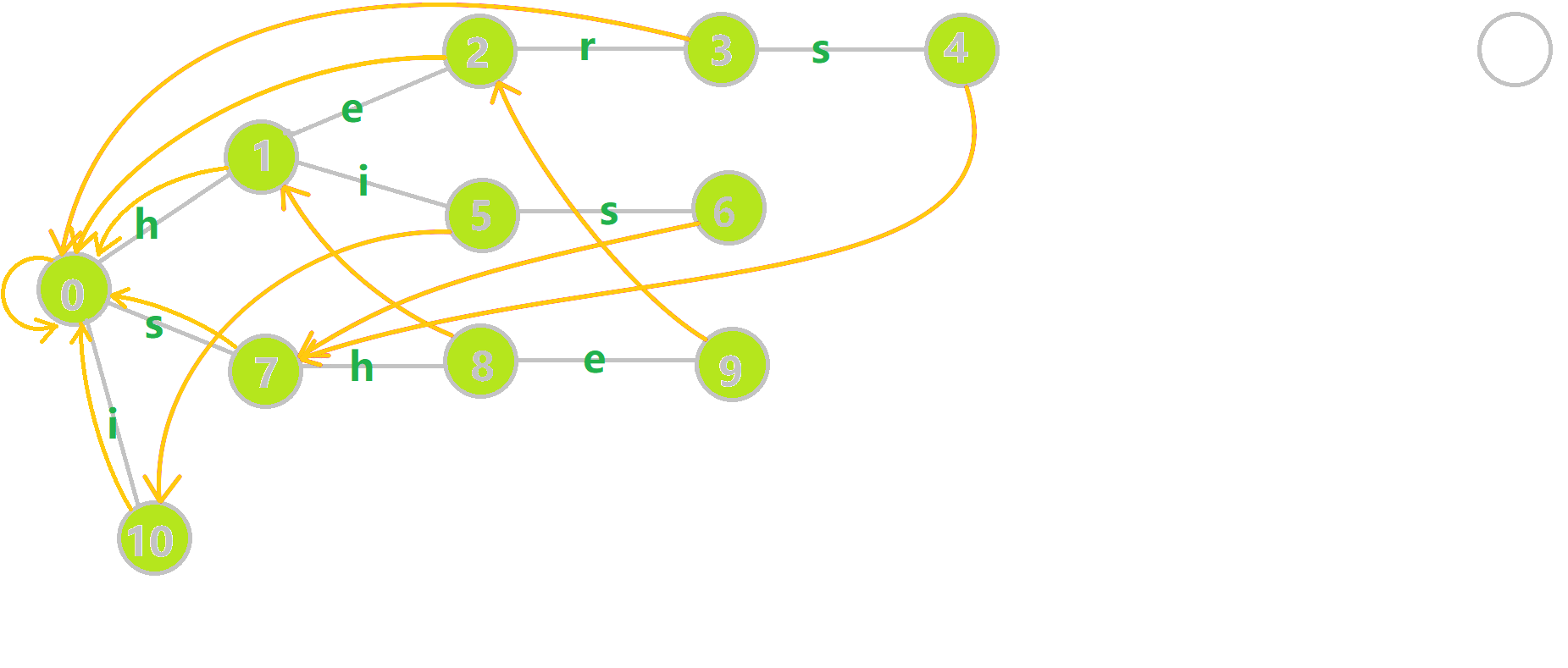
我们重点分析结点 6 的 fail 指针构建:
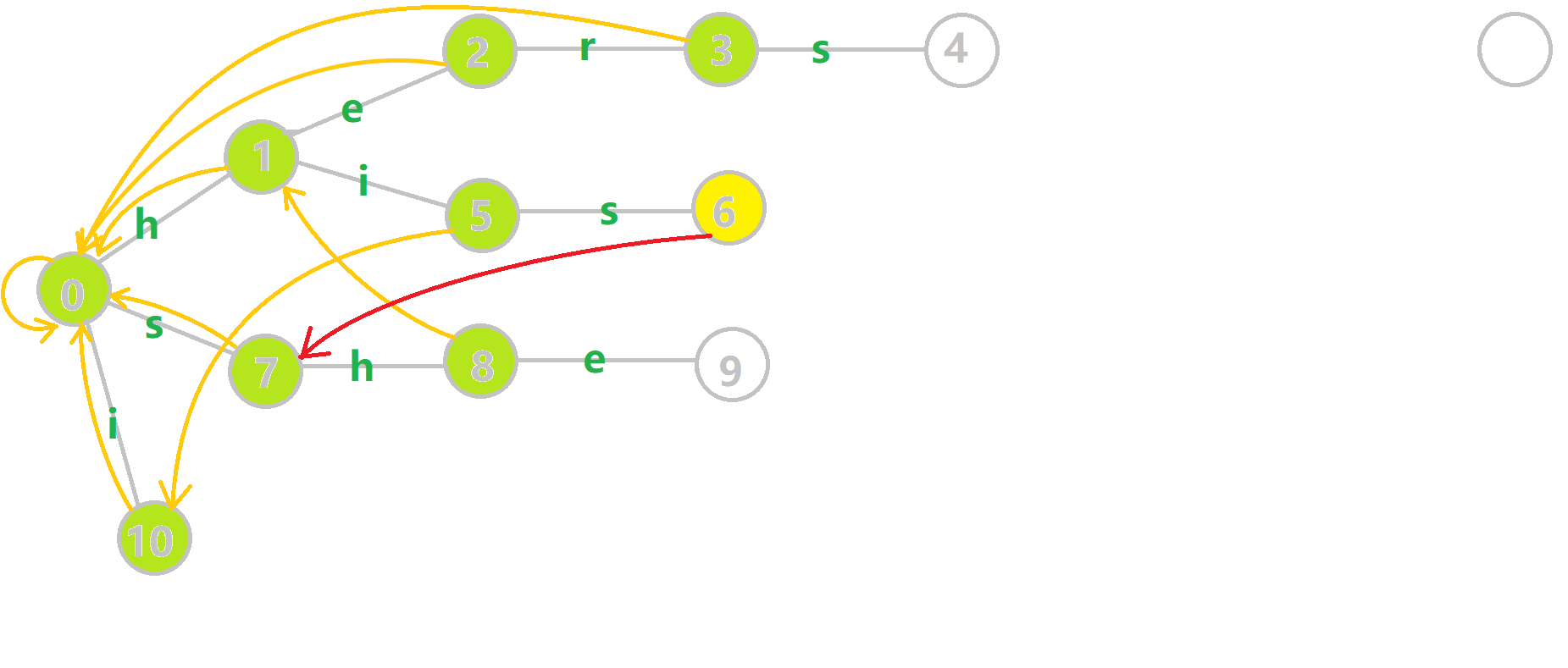
找到 6 的父结点 5,fail[5]=10