【问题】
求两个字符串 $S,T$ 的每个后缀的最长公共前缀。



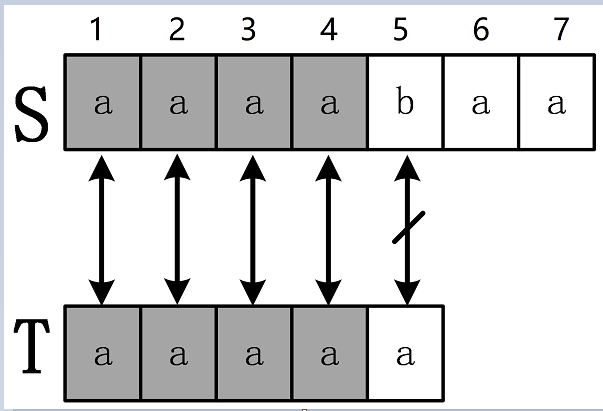
【定义】
对于一个长度为  $n$ 的字符串 $s$，定义函数 $z[i]$ 表示 $s$ 和 $s[i,n]$（即以 $s[i]$ 开头的后缀）的最长公共前缀（LCP）的长度，则 $z$ 被称为 $s$ 的 Z 函数。特别地，$z[0]=0$。

国外一般将计算该数组的算法称为 Z Algorithm，而国内则称其为 扩展KMP。

   i 1 2 3 4 5 6 7 8 9
   s a a a b a a a b c
z[i] 9 2 1 0 4 2 1 0 0

如上 $s=aaabaaabc$。那么
z[1]，为字符串 $s$ 和字符串 $s[1,9]$ 的 LCP。即 z[1]=9。
z[2]，为字符串 $s$ 和字符串 $s[2,9]$ 的 LCP。即 z[1]=9。


【解释】
下面样例

【模板代码】

/*
 * exKMP（Z函数）
 * z[i]表示字符串S与它第i个字符开始的后缀的最大公共前缀（LCP）长度
 * 时间复杂度：O(n)
 */
std::vector<int> z;
void exkmp(const std::string &s){
    int n=s.size()-1;
    //重置数组z数据
    z.assign(n+1,0);
    z[1]=n;
    for(int i=2,l=0,r=0; i<=n; i++){
        //初始化z
        if(i<=r){
            z[i]=min(z[i-l+1], r-i+1);
        }
        //暴力拓展
        while(s[i+z[i]]==s[1+z[i]]){
            z[i]++;
        }
        //更新最优区间
        if(i+z[i]-1>r){
            l=i;
            r=i+z[i]-1;
        }
    }
}