10141: ABC353 —— F - Tile Distance
[Creator : ]
Description
Tiles are laid out on a coordinate plane. There are two types of tiles: small tiles of size $1\times1$ and large tiles of size $K\times K$, laid out according to the following rules:
- For each pair of integers $(i,j)$, the square $\lbrace(x,y)\mid i\leq x\leq i+1\wedge j\leq y\leq j+1\rbrace$ is contained within either one small tile or one large tile.
- If $\left\lfloor\dfrac iK\right\rfloor+\left\lfloor\dfrac jK\right\rfloor$ is even, it is contained within a small tile.
- Otherwise, it is contained within a large tile.
Tiles include their boundaries, and no two different tiles have a positive area of intersection.
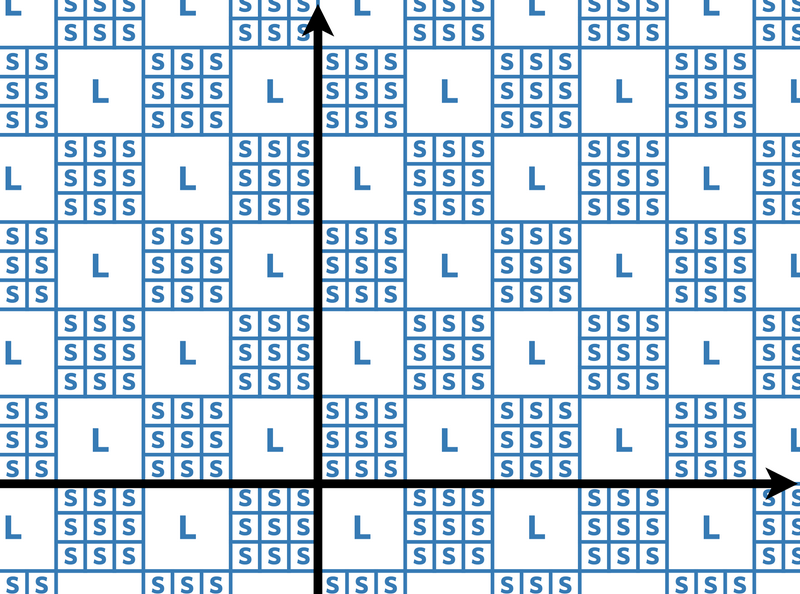
For example, when $K=3$, tiles are laid out as follows:
Takahashi starts at the point $(S_x+0.5,S_y+0.5)$ on the coordinate plane.
He can repeat the following movement any number of times:
- Choose a direction (up, down, left, or right) and a positive integer $n$. Move $n$ units in that direction.
Each time he crosses from one tile to another, he must pay a toll of $1$.
Determine the minimum toll Takahashi must pay to reach the point $(T_x+0.5,T_y+0.5)$.
- For each pair of integers $(i,j)$, the square $\lbrace(x,y)\mid i\leq x\leq i+1\wedge j\leq y\leq j+1\rbrace$ is contained within either one small tile or one large tile.
- If $\left\lfloor\dfrac iK\right\rfloor+\left\lfloor\dfrac jK\right\rfloor$ is even, it is contained within a small tile.
- Otherwise, it is contained within a large tile.
Tiles include their boundaries, and no two different tiles have a positive area of intersection.
For example, when $K=3$, tiles are laid out as follows:

Takahashi starts at the point $(S_x+0.5,S_y+0.5)$ on the coordinate plane.
He can repeat the following movement any number of times:
- Choose a direction (up, down, left, or right) and a positive integer $n$. Move $n$ units in that direction.
Each time he crosses from one tile to another, he must pay a toll of $1$.
Determine the minimum toll Takahashi must pay to reach the point $(T_x+0.5,T_y+0.5)$.
Input
The input is given from Standard Input in the following format:
```
$K$
$S_x$ $S_y$
$T_x$ $T_y$
```
```
$K$
$S_x$ $S_y$
$T_x$ $T_y$
```
Output
Print the minimum toll Takahashi must pay.
Constraints
- $1\leq K\leq10^{16}$
- $0\leq S_x\leq2\times10^{16}$
- $0\leq S_y\leq2\times10^{16}$
- $0\leq T_x\leq2\times10^{16}$
- $0\leq T_y\leq2\times10^{16}$
- All input values are integers.
- $0\leq S_x\leq2\times10^{16}$
- $0\leq S_y\leq2\times10^{16}$
- $0\leq T_x\leq2\times10^{16}$
- $0\leq T_y\leq2\times10^{16}$
- All input values are integers.
Sample 1 Input
3
7 2
1 6
Sample 1 Output
5
For example, he can move as follows, paying a toll of 5.
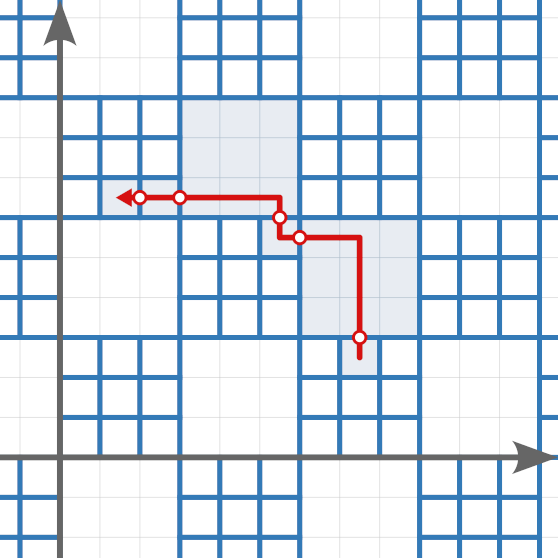
- Move up by 3. Pay a toll of 1.
- Move left by 2. Pay a toll of 1.
- Move up by 1. Pay a toll of 1.
- Move left by 4. Pay a toll of 2.
The toll paid cannot be 4 or less, so print 5.
Sample 2 Input
1
41 42
13 56
Sample 2 Output
42
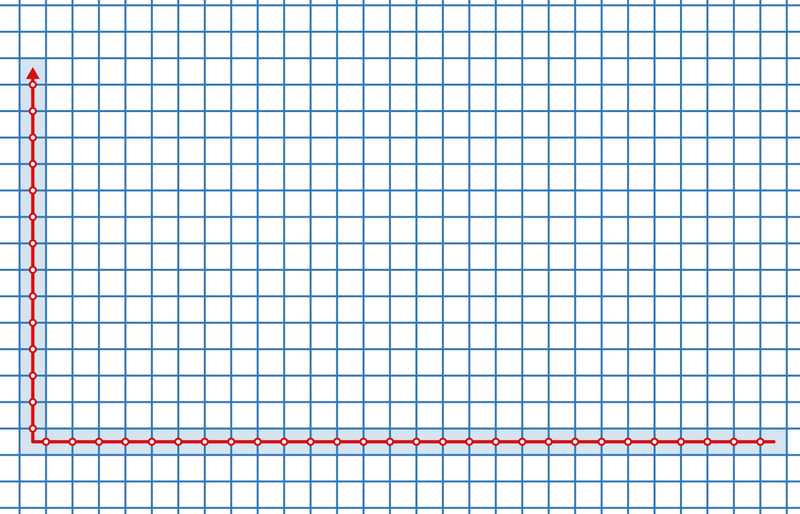
When he moves the shortest distance, he will always pay a toll of 42.
The toll paid cannot be 41 or less, so print 42.
Sample 3 Input
100
100 99
199 1
Sample 3 Output
0
There are cases where no toll needs to be paid.
96929423
5105216413055191 10822465733465225
1543712011036057 14412421458305526
79154049