10137: ABC353 —— B - AtCoder Amusement Park
[Creator : ]
Description
The AtCoder amusement park has an attraction that can accommodate $K$ people. Now, there are $N$ groups lined up in the queue for this attraction.
The $i$-th group from the front $(1\leq i\leq N)$ consists of $A_i$ people. For all $i$ $(1\leq i\leq N)$, it holds that $A_i \leq K$.
Takahashi, as a staff member of this attraction, will guide the groups in the queue according to the following procedure.
Initially, no one has been guided to the attraction, and there are $K$ empty seats.
1. If there are no groups in the queue, start the attraction and end the guidance.
2. Compare the number of empty seats in the attraction with the number of people in the group at the front of the queue, and do one of the following:
- If the number of empty seats is less than the number of people in the group at the front, start the attraction. Then, the number of empty seats becomes $K$ again.
- Otherwise, guide the entire group at the front of the queue to the attraction. The front group is removed from the queue, and the number of empty seats decreases by the number of people in the group.
3. Go back to step 1.
Here, no additional groups will line up after the guidance has started. Under these conditions, it can be shown that this procedure will end in a finite number of steps.
Determine how many times the attraction will be started throughout the guidance.
The $i$-th group from the front $(1\leq i\leq N)$ consists of $A_i$ people. For all $i$ $(1\leq i\leq N)$, it holds that $A_i \leq K$.
Takahashi, as a staff member of this attraction, will guide the groups in the queue according to the following procedure.
Initially, no one has been guided to the attraction, and there are $K$ empty seats.
1. If there are no groups in the queue, start the attraction and end the guidance.
2. Compare the number of empty seats in the attraction with the number of people in the group at the front of the queue, and do one of the following:
- If the number of empty seats is less than the number of people in the group at the front, start the attraction. Then, the number of empty seats becomes $K$ again.
- Otherwise, guide the entire group at the front of the queue to the attraction. The front group is removed from the queue, and the number of empty seats decreases by the number of people in the group.
3. Go back to step 1.
Here, no additional groups will line up after the guidance has started. Under these conditions, it can be shown that this procedure will end in a finite number of steps.
Determine how many times the attraction will be started throughout the guidance.
Input
The input is given from Standard Input in the following format:
```
$N$ $K$
$A_1$ $A_2$ $\ldots$ $A_N$
```
```
$N$ $K$
$A_1$ $A_2$ $\ldots$ $A_N$
```
Output
Print the answer.
Constraints
- $1\leq N\leq 100$
- $1\leq K\leq 100$
- $1\leq A_i\leq K\ (1\leq i\leq N)$
- All input values are integers.
- $1\leq K\leq 100$
- $1\leq A_i\leq K\ (1\leq i\leq N)$
- All input values are integers.
Sample 1 Input
7 6
2 5 1 4 1 2 3
Sample 1 Output
4
Initially, the seven groups are lined up as follows:

Part of Takahashi's guidance is shown in the following figure:
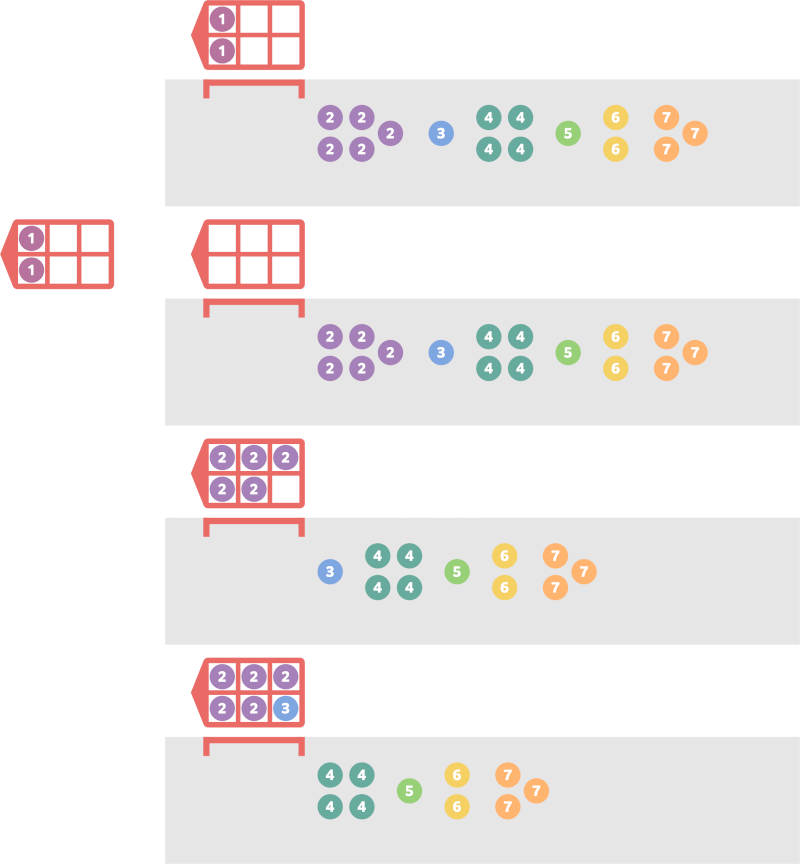
- Initially, the group at the front has 2 people, and there are 6 empty seats. Thus, he guides the front group to the attraction, leaving 4 empty seats.
- Next, the group at the front has 5 people, which is more than the 4 empty seats, so the attraction is started.
- After the attraction is started, there are 6 empty seats again, so the front group is guided to the attraction, leaving 1 empty seat.
- Next, the group at the front has 1 person, so they are guided to the attraction, leaving 0 empty seats.
In total, he starts the attraction four times before the guidance is completed. Therefore, print 4.

Sample 2 Input
7 10
1 10 1 10 1 10 1
Sample 2 Output
7
Sample 3 Input
15 100
73 8 55 26 97 48 37 47 35 55 5 17 62 2 60
Sample 3 Output
8