10129: ABC352 —— E - Clique Connect
[Creator : ]
Description
You are given a weighted undirected graph $G$ with $N$ vertices, numbered $1$ to $N$. Initially, $G$ has no edges.
You will perform $M$ operations to add edges to $G$. The $i$-th operation $(1 \leq i \leq M)$ is as follows:
- You are given a subset of vertices $S_i=\lbrace A_{i,1},A_{i,2},\dots,A_{i,K_i}\rbrace$ consisting of $K_i$ vertices. For every pair $u, v$ such that $u, v \in S_i$ and $u < v$, add an edge between vertices $u$ and $v$ with weight $C_i$.
After performing all $M$ operations, determine whether $G$ is connected. If it is, find the total weight of the edges in a minimum spanning tree of $G$.
You will perform $M$ operations to add edges to $G$. The $i$-th operation $(1 \leq i \leq M)$ is as follows:
- You are given a subset of vertices $S_i=\lbrace A_{i,1},A_{i,2},\dots,A_{i,K_i}\rbrace$ consisting of $K_i$ vertices. For every pair $u, v$ such that $u, v \in S_i$ and $u < v$, add an edge between vertices $u$ and $v$ with weight $C_i$.
After performing all $M$ operations, determine whether $G$ is connected. If it is, find the total weight of the edges in a minimum spanning tree of $G$.
Input
The input is given from Standard Input in the following format:
```
$N$ $M$
$K_1$ $C_1$
$A_{1,1}$ $A_{1,2}$ $\dots$ $A_{1,K_1}$
$K_2$ $C_2$
$A_{2,1}$ $A_{2,2}$ $\dots$ $A_{2,K_2}$
$\vdots$
$K_M$ $C_M$
$A_{M,1}$ $A_{M,2}$ $\dots$ $A_{M,K_M}$
```
```
$N$ $M$
$K_1$ $C_1$
$A_{1,1}$ $A_{1,2}$ $\dots$ $A_{1,K_1}$
$K_2$ $C_2$
$A_{2,1}$ $A_{2,2}$ $\dots$ $A_{2,K_2}$
$\vdots$
$K_M$ $C_M$
$A_{M,1}$ $A_{M,2}$ $\dots$ $A_{M,K_M}$
```
Output
If $G$ is not connected after all $M$ operations, print `-1`. If $G$ is connected, print the total weight of the edges in a minimum spanning tree of $G$.
Constraints
- $2 \leq N \leq 2 \times 10^5$
- $1 \leq M \leq 2 \times 10^5$
- $2 \leq K_i \leq N$
- $\sum_{i=1}^{M} K_i \leq 4 \times 10^5$
- $1 \leq A_{i,1} < A_{i,2} < \dots < A_{i,K_i} \leq N$
- $1 \leq C_i \leq 10^9$
- All input values are integers.
- $1 \leq M \leq 2 \times 10^5$
- $2 \leq K_i \leq N$
- $\sum_{i=1}^{M} K_i \leq 4 \times 10^5$
- $1 \leq A_{i,1} < A_{i,2} < \dots < A_{i,K_i} \leq N$
- $1 \leq C_i \leq 10^9$
- All input values are integers.
Sample 1 Input
4 3
3 3
1 2 3
2 2
1 2
3 4
1 3 4
Sample 1 Output
9
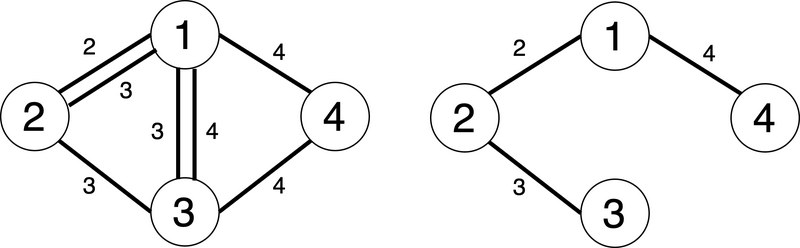
The left diagram shows G after all M operations, and the right diagram shows a minimum spanning tree of G (the numbers next to the edges indicate their weights).
The total weight of the edges in the minimum spanning tree is 3+2+4=9.
Sample 2 Input
3 2
2 1
1 2
2 1
1 2
Sample 2 Output
-1
G is not connected even after all M operations.
Sample 3 Input
10 5
6 158260522
1 3 6 8 9 10
10 877914575
1 2 3 4 5 6 7 8 9 10
4 602436426
2 6 7 9
6 24979445
2 3 4 5 8 10
4 861648772
2 4 8 9
Sample 3 Output
1202115217