There is an $N\times N$ grid where each cell contains an integer between $0$ and $5$, inclusive. Let $(i,j)$ denote the cell at the $i$-th row from the top and the $j$-th column from the left $(1\leq i,j\leq N)$. The integer written in cell $(i,j)$ is $A _ {i,j}$.

You can perform the following operation any number of times, possibly zero:

-   Choose a cell $(i,j)$ with $0$ written in it and an integer $x$ between $1$ and $5$, inclusive. Change the number written in the chosen cell to $x$.

After the operations, let $B _ {i,j}$ be the integer written in cell $(i,j)$. The cost of the grid is defined as the sum of the squares of the differences between the integers written in adjacent cells. In other words, the cost is represented by the following formula:

$\displaystyle\sum _ {i=1} ^ N\sum _ {j=1} ^ {N-1}(B _ {i,j}-B _ {i,j+1})^2+\sum _ {i=1} ^ {N-1}\sum _ {j=1} ^ N(B _ {i,j}-B _ {i+1,j})^2$

Among all possible states of the grid after the operations, find the one with the minimum cost.

If multiple grid states have the minimum cost, you may print any of them.

The input is given from Standard Input in the following format:

```
$N$
$A _ {1,1}$ $A _ {1,2}$ $\ldots$ $A _ {1,N}$
$A _ {2,1}$ $A _ {2,2}$ $\ldots$ $A _ {2,N}$
 $\vdots$   $\ \vdots$  $\ddots$  $\vdots$
$A _ {N,1}$ $A _ {N,2}$ $\ldots$ $A _ {N,N}$
```

Print $N$ lines. The $i$-th line $(1\leq i\leq N)$ should contain $B _ {i,1},B _ {i,2},\ldots,B _ {i,N}$ in this order, with spaces in between, after performing operations to minimize the cost.

-   $1\leq N\leq20$
-   $0\leq A _ {i,j}\leq 5\ (1\leq i\leq N,1\leq j\leq N)$
-   All input values are integers.

3 2 1 2 4
4 2 2 2 2
3 1 2 3 3
1 1 2 3 4
1 1 2 3 5

The given grid is as follows:



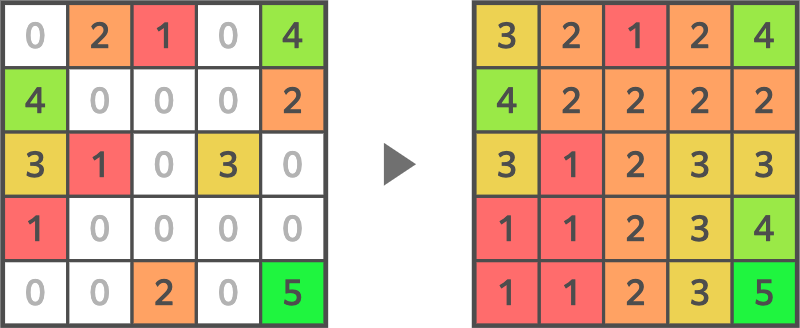
After performing operations to achieve the state shown on the right of the figure, the cost will be $2^2×6+1^2×18+0^2×16=42$.
The cost cannot be 41 or less, so printing the corresponding $B_{i,j}$ for this state would be accepted.

0 0 0
0 0 0
0 0 0

The cost is already 0 from the beginning, so not performing any operations minimizes the cost.
If multiple grid states have the minimum cost, you may print any of them, so the following output would also be accepted:

2 2 2
2 2 2
2 2 2