10095: ABC347 —— F - Non-overlapping Squares
[Creator : ]
Description
There is an $N\times N$ grid, and the cell at the $i$-th row from the top and the $j$-th column from the left $(1\leq i,j\leq N)$ contains the integer $A _ {i,j}$.
You are given an integer $M$. When choosing three non-overlapping $M\times M$ grids, find the maximum possible sum of the integers written in the chosen grids.
Formal definition of the problem A $6$\-tuple of integers $(i _ 1,j _ 1,i _ 2,j _ 2,i _ 3,j _ 3)$ is called a **good $6$\-tuple** when it satisfies the following three conditions:
- $1\leq i _ k\leq N-M+1\ (k=1,2,3)$
- $1\leq j _ k\leq N-M+1\ (k=1,2,3)$
- If $k\neq l\ (k,l\in\lbrace1,2,3\rbrace)$, the sets $\lbrace(i,j)\mid i _ k\leq i\lt i _ k+M\wedge j _ k\leq j\lt j _ k+M\rbrace$ and $\lbrace(i,j)\mid i _ l\leq i\lt i _ l+M\wedge j _ l\leq j\lt j _ l+M\rbrace$ do not intersect.
Find the maximum value of $\displaystyle \sum _ {k=1} ^ 3\sum _ {i=i _ k} ^ {i _ k+M-1}\sum _ {j=j _ k} ^ {j _ k+M-1}A _ {i,j}$ for a good $6$\-tuple $(i _ 1,j _ 1,i _ 2,j _ 2,i _ 3,j _ 3)$. It can be shown that a good $6$\-tuple exists under the constraints of this problem.
You are given an integer $M$. When choosing three non-overlapping $M\times M$ grids, find the maximum possible sum of the integers written in the chosen grids.
Formal definition of the problem A $6$\-tuple of integers $(i _ 1,j _ 1,i _ 2,j _ 2,i _ 3,j _ 3)$ is called a **good $6$\-tuple** when it satisfies the following three conditions:
- $1\leq i _ k\leq N-M+1\ (k=1,2,3)$
- $1\leq j _ k\leq N-M+1\ (k=1,2,3)$
- If $k\neq l\ (k,l\in\lbrace1,2,3\rbrace)$, the sets $\lbrace(i,j)\mid i _ k\leq i\lt i _ k+M\wedge j _ k\leq j\lt j _ k+M\rbrace$ and $\lbrace(i,j)\mid i _ l\leq i\lt i _ l+M\wedge j _ l\leq j\lt j _ l+M\rbrace$ do not intersect.
Find the maximum value of $\displaystyle \sum _ {k=1} ^ 3\sum _ {i=i _ k} ^ {i _ k+M-1}\sum _ {j=j _ k} ^ {j _ k+M-1}A _ {i,j}$ for a good $6$\-tuple $(i _ 1,j _ 1,i _ 2,j _ 2,i _ 3,j _ 3)$. It can be shown that a good $6$\-tuple exists under the constraints of this problem.
Input
The input is given from Standard Input in the following format:
```
$N$ $M$
$A _ {1,1}$ $A _ {1,2}$ $\ldots$ $A _ {1,N}$
$A _ {2,1}$ $A _ {2,2}$ $\ldots$ $A _ {2,N}$
$\vdots$ $\ \vdots$ $\ddots$ $\vdots$
$A _ {N,1}$ $A _ {N,2}$ $\ldots$ $A _ {N,N}$
```
```
$N$ $M$
$A _ {1,1}$ $A _ {1,2}$ $\ldots$ $A _ {1,N}$
$A _ {2,1}$ $A _ {2,2}$ $\ldots$ $A _ {2,N}$
$\vdots$ $\ \vdots$ $\ddots$ $\vdots$
$A _ {N,1}$ $A _ {N,2}$ $\ldots$ $A _ {N,N}$
```
Output
Print the answer.
Constraints
- $2\leq N\leq 1000$
- $1\leq M\leq N/2$
- $0\leq A _ {i,j}\leq10 ^ 9$
- All input values are integers.
- $1\leq M\leq N/2$
- $0\leq A _ {i,j}\leq10 ^ 9$
- All input values are integers.
Sample 1 Input
7 3
3 1 4 1 5 9 2
6 5 3 5 8 9 7
9 3 2 3 8 4 6
2 6 4 3 3 8 3
2 7 9 5 0 2 8
8 4 1 9 7 1 6
9 3 9 9 3 7 5
Sample 1 Output
154
From the given grid, if we choose three 3×3 grids as shown in the figure below (this corresponds to setting $(i_1,j_1,i_2,j_2,i_3,j_3)=(1,5,2,1,5,2)$), the sum of the numbers written in the chosen grids will be 154.
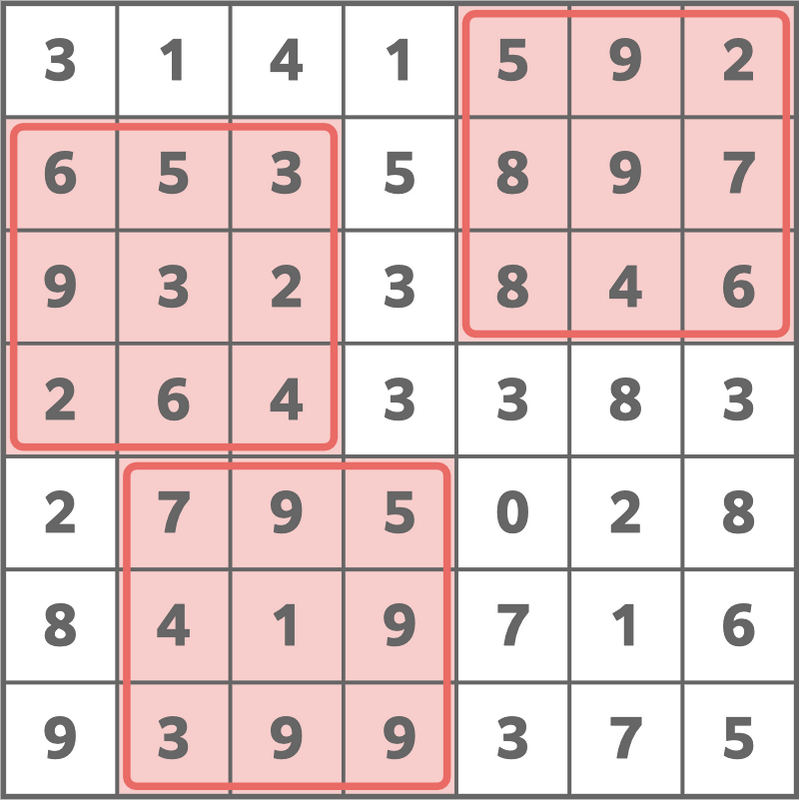
There is no way to make the sum 155 or greater while satisfying the conditions in the problem statement, so print 154.

There is no way to make the sum 155 or greater while satisfying the conditions in the problem statement, so print 154.
Sample 2 Input
7 1
3 1 4 1 5 9 2
6 5 3 5 8 9 7
9 3 2 3 8 4 6
2 6 4 3 3 8 3
2 7 9 5 0 2 8
8 4 1 9 7 1 6
9 3 9 9 3 7 5
Sample 2 Output
27
The following choice is optimal.


Sample 3 Input
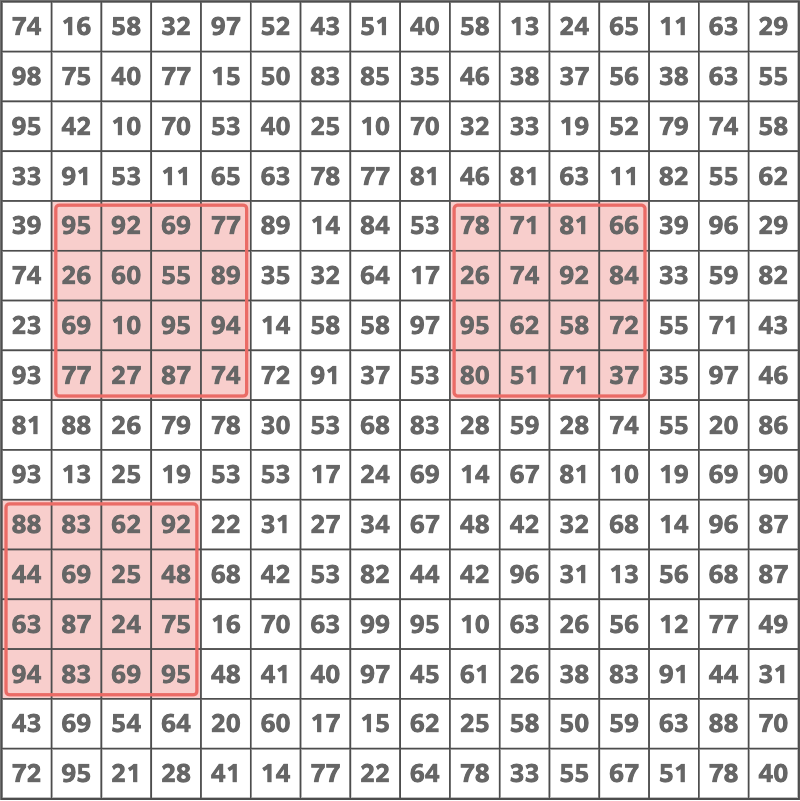
16 4
74 16 58 32 97 52 43 51 40 58 13 24 65 11 63 29
98 75 40 77 15 50 83 85 35 46 38 37 56 38 63 55
95 42 10 70 53 40 25 10 70 32 33 19 52 79 74 58
33 91 53 11 65 63 78 77 81 46 81 63 11 82 55 62
39 95 92 69 77 89 14 84 53 78 71 81 66 39 96 29
74 26 60 55 89 35 32 64 17 26 74 92 84 33 59 82
23 69 10 95 94 14 58 58 97 95 62 58 72 55 71 43
93 77 27 87 74 72 91 37 53 80 51 71 37 35 97 46
81 88 26 79 78 30 53 68 83 28 59 28 74 55 20 86
93 13 25 19 53 53 17 24 69 14 67 81 10 19 69 90
88 83 62 92 22 31 27 34 67 48 42 32 68 14 96 87
44 69 25 48 68 42 53 82 44 42 96 31 13 56 68 83
63 87 24 75 16 70 63 99 95 10 63 26 56 12 77 49
94 83 69 95 48 41 40 97 45 61 26 38 83 91 44 31
43 69 54 64 20 60 17 15 62 25 58 50 59 63 88 70
72 95 21 28 41 14 77 22 64 78 33 55 67 51 78 40
Sample 3 Output
3295
The following choice is optimal.