10073: ABC343 —— E - 7x7x7
[Creator : ]
Description
> In a coordinate space, we want to place three cubes with a side length of $7$ so that the volumes of the regions contained in exactly one, two, three cube(s) are $V_1$, $V_2$, $V_3$, respectively.
For three integers $a$, $b$, $c$, let $C(a,b,c)$ denote the cubic region represented by $(a\leq x\leq a+7) \land (b\leq y\leq b+7) \land (c\leq z\leq c+7)$.
Determine whether there are nine integers $a_1, b_1, c_1, a_2, b_2, c_2, a_3, b_3, c_3$ that satisfy all of the following conditions, and find one such tuple if it exists.
- $|a_1|, |b_1|, |c_1|, |a_2|, |b_2|, |c_2|, |a_3|, |b_3|, |c_3| \leq 100$
- Let $C_i = C(a_i, b_i, c_i)\ (i=1,2,3)$.
- The volume of the region contained in exactly one of $C_1, C_2, C_3$ is $V_1$.
- The volume of the region contained in exactly two of $C_1, C_2, C_3$ is $V_2$.
- The volume of the region contained in all of $C_1, C_2, C_3$ is $V_3$.
For three integers $a$, $b$, $c$, let $C(a,b,c)$ denote the cubic region represented by $(a\leq x\leq a+7) \land (b\leq y\leq b+7) \land (c\leq z\leq c+7)$.
Determine whether there are nine integers $a_1, b_1, c_1, a_2, b_2, c_2, a_3, b_3, c_3$ that satisfy all of the following conditions, and find one such tuple if it exists.
- $|a_1|, |b_1|, |c_1|, |a_2|, |b_2|, |c_2|, |a_3|, |b_3|, |c_3| \leq 100$
- Let $C_i = C(a_i, b_i, c_i)\ (i=1,2,3)$.
- The volume of the region contained in exactly one of $C_1, C_2, C_3$ is $V_1$.
- The volume of the region contained in exactly two of $C_1, C_2, C_3$ is $V_2$.
- The volume of the region contained in all of $C_1, C_2, C_3$ is $V_3$.
Input
The input is given from Standard Input in the following format:
```
$V_1$ $V_2$ $V_3$
```
```
$V_1$ $V_2$ $V_3$
```
Output
If no nine integers $a_1, b_1, c_1, a_2, b_2, c_2, a_3, b_3, c_3$ satisfy all of the conditions in the problem statement, print `No`. Otherwise, print such integers in the following format. If multiple solutions exist, you may print any of them.
```
Yes
$a_1$ $b_1$ $c_1$ $a_2$ $b_2$ $c_2$ $a_3$ $b_3$ $c_3$
```
```
Yes
$a_1$ $b_1$ $c_1$ $a_2$ $b_2$ $c_2$ $a_3$ $b_3$ $c_3$
```
Constraints
- $0 \leq V_1, V_2, V_3 \leq 3 \times 7^3$
- All input values are integers.
- All input values are integers.
Sample 1 Input
840 84 7
Sample 1 Output
Yes
0 0 0 0 6 0 6 0 0
Consider the case $(a_1,b_1,c_1,a_2,b_2,c_2,a_3,b_3,c_3)=(0,0,0,0,6,0,6,0,0)$.
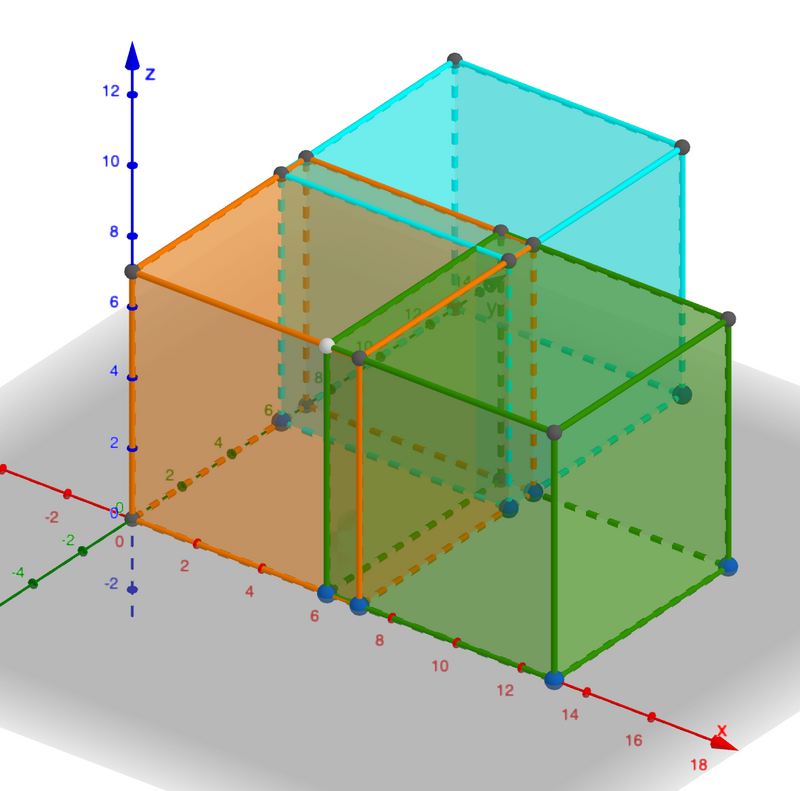
The figure represents the positional relationship of $C_1, C_2$, and $C_3$, corresponding to the orange, cyan, and green cubes, respectively.
Here,
$(a_1,b_1,c_1,a_2,b_2,c_2,a_3,b_3,c_3)=(−10,0,0,−10,0,6,−10,6,1)$ also satisfies all conditions and would be a valid output.

The figure represents the positional relationship of $C_1, C_2$, and $C_3$, corresponding to the orange, cyan, and green cubes, respectively.
Here,
- All of $∣a_1∣,∣b_1∣,∣c_1∣,∣a_2∣,∣b_2∣,∣c_2∣,∣a_3∣,∣b_3∣,∣c_3∣$ are not greater than 100.
- The region contained in all of $C_1,C_2,C_3$ is (6≤x≤7)∧(6≤y≤7)∧(0≤z≤7), with a volume of (7−6)×(7−6)×(7−0)=7.
- The region contained in exactly two of $C_1,C_2,C_3$ is ((0≤x<6)∧(6≤y≤7)∧(0≤z≤7))∨((6≤x≤7)∧(0≤y<6)∧(0≤z≤7)), with a volume of (6−0)×(7−6)×(7−0)×2=84.
- The region contained in exactly one of $C_1,C_2,C_3$ has a volume of 840.
$(a_1,b_1,c_1,a_2,b_2,c_2,a_3,b_3,c_3)=(−10,0,0,−10,0,6,−10,6,1)$ also satisfies all conditions and would be a valid output.
Sample 2 Input
343 34 3
Sample 2 Output
No
No nine integers $a_1,b_1,c_1,a_2,b_2,c_2,a_3,b_3,c_3$ satisfy all of the conditions.