In the country of AtCoder, there are $N$ stations: station $1$, station $2$, $\ldots$, station $N$.

You are given $M$ pieces of information about trains in the country. The $i$-th piece of information $(1\leq i\leq M)$ is represented by a tuple of six positive integers $(l _ i,d _ i,k _ i,c _ i,A _ i,B _ i)$, which corresponds to the following information:

-   For each $t=l _ i,l _ i+d _ i,l _ i+2d _ i,\ldots,l _ i+(k _ i-1)d _ i$, there is a train as follows:
    -   The train departs from station $A _ i$ at time $t$ and arrives at station $B _ i$ at time $t+c _ i$.

No trains exist other than those described by this information, and it is impossible to move from one station to another by any means other than by train.  
Also, assume that the time required for transfers is negligible.

Let $f(S)$ be the latest time at which one can arrive at station $N$ from station $S$.  
More precisely, $f(S)$ is defined as the maximum value of $t$ for which there is a sequence of tuples of four integers $\big((t _ i,c _ i,A _ i,B _ i)\big) _ {i=1,2,\ldots,k}$ that satisfies all of the following conditions:

-   $t\leq t _ 1$
-   $A _ 1=S,B _ k=N$
-   $B _ i=A _ {i+1}$ for all $1\leq i\lt k$,
-   For all $1\leq i\leq k$, there is a train that departs from station $A _ i$ at time $t _ i$ and arrives at station $B _ i$ at time $t _ i+c _ i$.
-   $t _ i+c _ i\leq t _ {i+1}$ for all $1\leq i\lt k$.

If no such $t$ exists, set $f(S)=-\infty$.

Find $f(1),f(2),\ldots,f(N-1)$.

The input is given from Standard Input in the following format:

```
$N$ $M$
$l _ 1$ $d _ 1$ $k _ 1$ $c _ 1$ $A _ 1$ $B _ 1$
$l _ 2$ $d _ 2$ $k _ 2$ $c _ 2$ $A _ 2$ $B _ 2$
$\vdots$
$l _ M$ $d _ M$ $k _ M$ $c _ M$ $A _ M$ $B _ M$
```

Print $N-1$ lines. The $k$-th line should contain $f(k)$ if $f(k)\neq-\infty$, and `Unreachable` if $f(k)=-\infty$.

-   $2\leq N\leq2\times10 ^ 5$
-   $1\leq M\leq2\times10 ^ 5$
-   $1\leq l _ i,d _ i,k _ i,c _ i\leq10 ^ 9\ (1\leq i\leq M)$
-   $1\leq A _ i,B _ i\leq N\ (1\leq i\leq M)$
-   $A _ i\neq B _ i\ (1\leq i\leq M)$
-   All input values are integers.

55
56
58
60
17

The following diagram shows the trains running in the country (information about arrival and departure times is omitted).

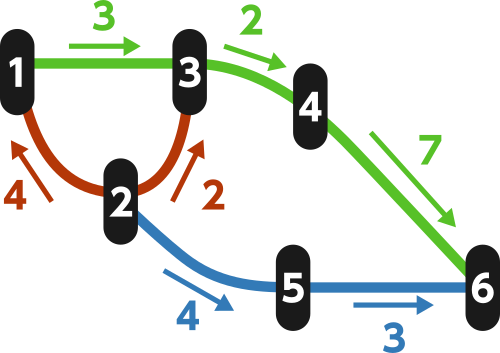
Consider the latest time at which one can arrive at station 6 from station 2. As shown in the following diagram, one can arrive at station 6 by departing from station 2 at time 56 and moving as station 2→ station 3→ station 4→ station 6.

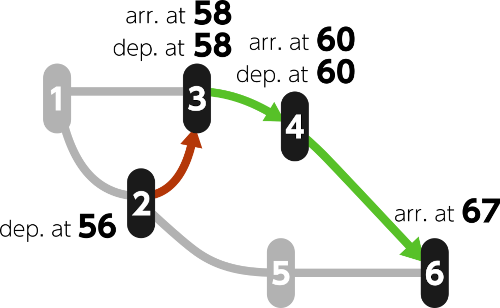
It is impossible to depart from station 2 after time 56 and arrive at station 6, so f(2)=56.

1000000000000000000
Unreachable
1
Unreachable

There is a train that departs from station 1 at time $10^{18}$ and arrives at station 5 at time $10^{18}+10^{9}$. There are no trains departing from station 1 after that time, so $f(1)=10^{18}$. As seen here, the answer may not fit within a ⁡32bit integer.
Also, both the second and third pieces of information guarantee that there is a train that departs from station 2 at time 14 and arrives at station 3 at time 20. As seen here, some trains may appear in multiple pieces of information.