You are given a tree $T$ with $N$ vertices: vertex $1$, vertex $2$, $\ldots$, vertex $N$. The $i$-th edge $(1\leq i\lt N)$ connects vertices $u_i$ and $v_i$.

For a vertex $u$ in $T$, define $f(u)$ as follows:

-   $f(u):=$ The number of pairs of vertices $v$ and $w$ in $T$ that satisfy the following two conditions:
    -   Vertex $w$ is contained in the path connecting vertices $u$ and $v$.
    -   $v\lt w$.

Here, vertex $w$ is contained in the path connecting vertices $u$ and $v$ also when $u=w$ or $v=w$.

Find the values of $f(1),f(2),\ldots,f(N)$.

The input is given from Standard Input in the following format:

```
$N$
$u_1$ $v_1$
$u_2$ $v_2$
$\vdots$
$u_{N-1}$ $v_{N-1}$
```

Print the values of $f(1),f(2),\ldots,f(N)$ in this order, separated by spaces.

-   $2\leq N\leq2\times10^5$
-   $1\leq u_i\leq N\ (1\leq i\leq N)$
-   $1\leq v_i\leq N\ (1\leq i\leq N)$
-   The given graph is a tree.
-   All input values are integers.

0 1 3 4 8 9 15

The given tree is as follows:

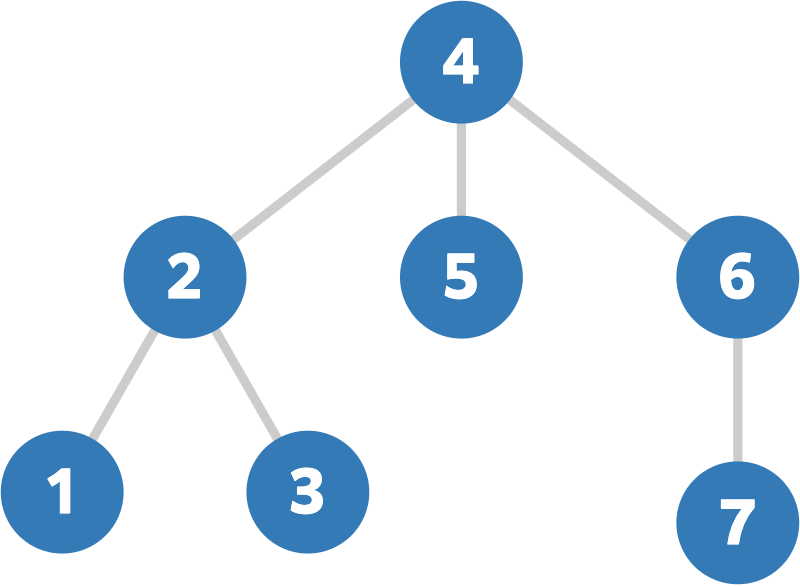
For example, f(4)=4. Indeed, for u=4, four pairs (v,w)=(1,2),(1,4),(2,4),(3,4) satisfy the conditions.

36 29 32 29 48 37 45 37 44 42 33 36 35 57 35

The given tree is as follows:

The value of f(14) is 57, which is the inversion number of the sequence (14,9,1,6,12,2,15,4,11,13,3,8,10,7,5).