Problem F: §3 3 小球(drop)
[Creator : ]
Description
许多的小球一个一个的从一棵满二叉树上掉下来组成 FBT(Full Binary
Tree,满二叉树),每一时间,一个正在下降的球第一个访问的是非叶子节点。然后继续下降时,或者走右子树,或者走左子树,直到访问到叶子节点。决定球运动方向的是每个节点的布尔值。最初,所有的节点都是 false,当访问到一个节点时,如果这个节点是 false,则这个球把它变成 true,然后从左子树走,继续它的旅程。如果节点是 true,则球也会改变它为 false,而接下来从右子树走。满二叉树的标记方法如下图:
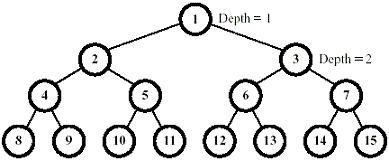
因为所有的节点最初为 false,所以第一个球将会访问节点 $1$,节点 $2$ 和节点 $4$,转变节点的布尔值后在在节点8停止。第二个球将会访问节点 $1,\ 3,\ 6$,在节点 $12$ 停止。明显地,第三个球在它停止之前,会访问节点 $1,\ 2,\ 5$,在节点 $10$ 停止。
现在你的任务是,给定 FBT 的深度 $D$,和 $I$,表示第 $I$ 个小球下落,你可以假定 $I$ 不超过给定的 FBT 的叶子数,写一个程序求小球停止时的叶子序号。

因为所有的节点最初为 false,所以第一个球将会访问节点 $1$,节点 $2$ 和节点 $4$,转变节点的布尔值后在在节点8停止。第二个球将会访问节点 $1,\ 3,\ 6$,在节点 $12$ 停止。明显地,第三个球在它停止之前,会访问节点 $1,\ 2,\ 5$,在节点 $10$ 停止。
现在你的任务是,给定 FBT 的深度 $D$,和 $I$,表示第 $I$ 个小球下落,你可以假定 $I$ 不超过给定的 FBT 的叶子数,写一个程序求小球停止时的叶子序号。
Input
一行包含两个用空格隔开的整数 $D$ 和 $I$。其中 $2≤D≤20, 1≤I≤524,288$。
Output
对应输出第 $I$ 个小球下落停止时的叶子序号。
Sample 1 Input
4 2
Sample 1 Output
12